Wieso ist in jedem rechtwinkligem Dreieck die Seitenhalbierende der Hypotenuse halb so lang wie diese?

Diese Aufgabe hat mir mein Mathe-Lehrer geschickt. Ich verstehe die Aufgabe nicht. Kann mir jemand helfen?
5 Antworten
Ein rechtwinkliges Dreieck ist immer ein diagonal geteiltes Rechteck. Die Hypotenuse ist dabei die Diagonale. Und die Seitenhalbierende dieser Hypothenuse ist in der Verlängerung die andere Diagonale im Rechteck. Und da sich beide in der Mitte überkreuzen, sind die beiden Diagonalen jeweils zu Hälfte geteilt.
„Zeichnung und Erläuterungen“ - Hast du denn bereits eine Zeichnung/Skizze dazu gemacht? Dann sollte das evtl. klarer/übersichtlicher werden.
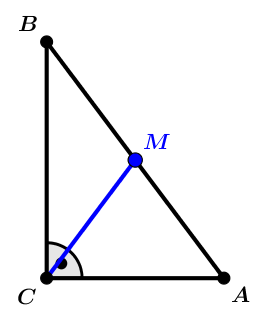
Bemerkungen:
- Das Dreieck ABC ist rechtwinklig mit rechtem Winkel bei C. Die Seite [AB] ist die Hypotenuse dieses rechtwinkligen Dreiecks.
- M ist der Mittelpunkt der Hypotenuse [AB]. Die Strecke [CM] ist dementsprechend die Seitenhalbierende der Hypotenuse.
- Es soll nun gezeigt werden, dass [CM] in solch einem Fall immer halb so lang wie [AB] ist.
============
Hinweis 1: Finde ein gleichschenkliges Dreieck.
Hinweis 2: Du könntest zeigen, dass das Dreieck AMC (bzw. auch das Dreieck BCM) gleichschenklig ist, also die Schenkel [AM] und [CM] des gleichschenkligen Dreiecks AMC gleich lang sind.
Hinweis 3: Auf einem Kreis haben alle Punkte den gleichen Abstand zum Kreismittelpunkt.
Hinweis 4: Was für ein speziellen Kreis (hat sogar einen Namen) fällt dir ein, wenn es um rechtwinklige Dreiecke geht?
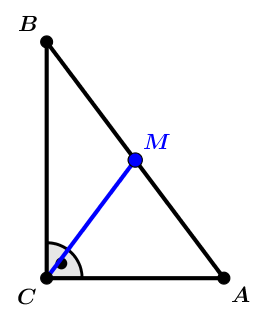
Hallo,
zwei Tipps: Thaleskreis und Gleichschenkligkeit (Radien).
Herzliche Grüße,
Willy
Kennst Du schon den Satz des Thales?
Jedes Dreieck im Halbkreis ist ein rechtes...
Dadurch ist die Hypotenuse immer der Kreisdurchmesser und die Seitenhalbierende ein Radius.
Tipp: Thaleskreis