Wie komme ich von dem Scheitelpunktform zur Nullstellenform und anders rum?

Ich benenne das mal um, damit man nicht denkt e wäre die Eulersche Zahl :

a * (x - u) ^ 2 + v = a * (x - f) * (x - g)

b = -2 * a * u

c = a * u ^ 2 + v


f  = (- b - √(b ^ 2 – 4 * a * c) ) / (2 * a)


g = ( - b + √(b ^ 2 – 4 * a * c) ) / (2 * a)

Beispiel :

2 * (x + 2) ^ 2 - 10

a = 2 und u = - 2 und v = -10

b = -2 * 2 * -2 = 8

c = 2 * (-2) ^ 2 - 10 = -2

f = (- 8 - √(8 ^ 2 - 4 * 2 * -2)) / (2 * 2) = -4.23606797749979...

g = (- 8 + √(8 ^ 2 - 4 * 2 * -2)) / (2 * 2) = 0.2360679774997898...

Also gilt jetzt :

2 * (x + 2) ^ 2 - 10 = 2 * (x - ( -4.23606797749979...)) * (x - 0.2360679774997898...)

2 * (x + 2) ^ 2 - 10 = 2 * (x + 4.23606797749979...) * (x - 0.2360679774997898...)

Nur innerhalb der Rundungsfehler genau, weil es Zahlen mit unendlich vielen Stellen nach dem Komma sind.

Über den Rückweg, also von der Form a * (x - f) * (x - g) wieder auf die Form a * (x - u) ^ 2 + v zu kommen, konnte ich mir aufgrund von Zeitmangel noch keine Gedanken machen, sorry.


Sei die Funktion : 3(x+2)(x-5) gegeben

Man siehst hier die sogenannte: "Nullstellenform"

Nullstelle bei : x1 = -2 und x2 = 5

So von der Nullstellenform zur Parameterform

(Einfach ausmultiplizieren:

3(x+2)(x-5)

3(x^2-5x+2x-10)
3x^2 -15x + 6x -30
3x^2 -9x -30 = y

Nun mit der quadratischen Ergänzung in die Scheitelpunktform umwandeln

y = 3x^2 -9x -30
y = 3(x^2-3x)-30
y = 3(x^2-3x + 1,5^2-1,5^2) -30
y = 3(x^2-3x + 2,25) +3*(-2,25)-30
y = 3(x-1,5)^2 -36,75

S(1,5/-36,75)

Die Nullstellen herausfinden und die Nullstellenform aufstellen (wenn es welche gibt).

y = 3(x-1,5)^2 -36,75  y = 0

0 = 3(x-1,5)^2 -36,75 | + 36,75
36,75 = 3(x-1,5)^2 | :3
12,25 = (x-1,5)^2 | √
3,5 = x-1,5 | +1,5
-3,5 = x-1,5 | + 1,5

x1 = 5
x2 = -2

Aufstellen der Nullstellenform:

3(x+2)(x-5)

Und wie man sieht wie am Anfang.

Dabei gilt :

Wenn bei der Scheitelpunktform e positiv ist hätte man :

Bsp ( x+3)^2 + 9 = 0 | -9
        (x+3)^2 = -9 | √

Hier würde es nicht weitergehen. Also keine reellen Nullstellen.

Anderes Beispiel:

(x+3) = 0 | √
x+3 = 0 | -3

x1 = -3

Eine Nullstelle.

So würde ich es prinzipiell machen, gibt sicher andere Wege, aber hier ein möglicher Weg.

Wenn du ein Beispiel hättest, könnten wir es zusammen durchgehen.

Also zusammenfassend :

Scheitelpunktform => Nullstellenform

Durch Berechnung

Nullstellenform => Parameterform => Scheitelpunktform =>

Ausmultiplizieren => quadratische Ergänzung

Müsste alles erwähnt haben.

Unten steht jetzt eine Antwort mit Formeln. Wie gesagt, möglicher Weg.

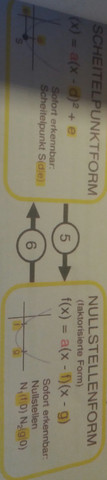
allgemeine Form: f(x)=ax²+bx+c

Nullstellen: x1,2=[-b±√(b²-4ac)]/2a

Nullstellenform: f(x)=a(x-x1)(x-x2)

Scheitelpunkt: x_s=-b/2a     y_s=f(x_s)=b²/4a-b²/2a+c

Scheitelpunktform: f(x)=a(x-x_s)²+y_s

Oder ersichtlicher von SP-Form in Nullstellenform:

a(x1,2-x_s)²+y_s=0  (Das gibt wieder die Nullstellen x1,2)

(x1,2-x_s)²=-y_s/a

x1,2-x_s=±√(-y_s/a)

x1,2=±√(-y_s/a)-x_s

NS-Form in SP-Form:

a(x-x1)(x-x2)=a[x²-x*(x1+x2)+x1*x2]=

=a[x²-x*(x1+x2)+(x1+x2)²/4-(x1+x2)²/4+x1*x2]=

=a[(x-(x1+x2)/2)²-(x1²-2*x1*x2+x2²)/4]

Damit: x_s=(x1+x2)/2 und y_s=-a/4*(x1²-2*x1*x2+x2²)=-a/4 * (x1-x2)²

Kontrolle: a((x1+x2)/2-x1)((x1+x2)/2-x2)=a(x2-x1)(x1-x2)/4=

=-a/4*[-2x1*x2+x1²+x2²]=-a/4 * (x1-x2)²=y_s

Zusammenfassend kannst du dir folgende vier Formeln merken:

f(x)=a(x-x1)(x-x2)

f(x)=a(x-x_s)²+y_s

x1=√(-y_s/a)-x_s

x2=-√(-y_s/a)-x_s

x_s=(x1+x2)/2

y_s=-a/4 * (x1-x2)²