Wie kann man an diese Aufgabe herangehen?
Ich habe Probleme damit diese Aufgabe zu lösen. Man soll diese Eigenschaft eines Dreiecks (siehe Bilder) beweisen. Ich möchte keine Lösung haben, nur wie man die Aufgabe angehen kann (und eventuell generell Strategien für solche Aufgabentypen).
Vielen Dank schon mal für Antworten!


3 Antworten
1) Da nach einem Zusammenhang zwischen einem Dreieckswinkel und seiner gegenüberliegenden Seite gefragt ist, wühlen wir mal die diversen geometrischen Formeln durch, ob wir was passende finden.
2) Dabei fällt uns der Kosinussatz ins Auge.

Den prüfen wir mal etwas näher auf Brauchbarkeit, indem wir schauen, ob die Werte in den Formeln gegebene sind.
3) Nun stellen wir fest, dass die beiden anderen Seiten gegeben bzw. fest sind. Also können wir den Kosinussatz gebrauchen.
4) Statt α setzen wir nun ein: α + Δα und erhalten:
L + ΔL = d1^2 + d2^2 - 2d1*d2 * cos(α + Δα)
5) Das lösen wir nach ΔL auf, wobei sicherlich noch der eine oder andere geometrische Satz herhalten muss, um auf die vorgegebene Formel zu kommen.
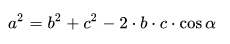
Stichwort Kosinussatz. Geometrieaufgaben erfordern immer eine ganz eigene Herangehensweise, ein einfaches Rezept gibt es in der Regel nicht, obwohl man, wenn man häufig solche Aufgaben löst, durchaus Ähnlichkeiten feststellt. :)
Mittels der Gaußschen Fehlerfortpflanzung (Funktion aufstellen, partiell ableiten, totales Differential, Fehlerfortpflanzung), ausgehend vom Kosinussatz, lässt sich der Zusammenhang herleiten.
... manchmal bin ich froh, dass Physiker da mathematisch auch mal eher lockerer unterwegs sind ;-)
(L + ΔL)^2