3 Antworten
Klammere einen der Summanden aus, also entweder [x] oder wurzel(x), und versuche danach nochmal den Grenzwert zu bestimmen!
Also ich würde sagen, dass es intuitiv klar ist, dass der Ausdruck divergiert.
Um das zu beweisen kannst du folgende abschätzung nutzen:
floor(x)>= x-1 (floor = Gaußklammer)
Somit erhälst du: floor(x)-wurzel(x)>=x-1-wurzel(x)
Das kannst du umschreiben zu:
wurzel(x)(wurzel(x)-1) -1
Folgere nun, dass die Abschätzung gegen unendlich geht, weswegen dein Ausdruck auch gegen unendlich gehen muss.
Die Bestandteile dieser Funktion kannst du ja einzeln betrachten. Also [x] läuft gegen Plus unendlich und sqrt(x) läuft gegen Plus unendlich
Und genau wegen diesem Grund darf man das hier nicht, da ∞-∞ ein unbestimmter Ausdruck ist, der jeden Wert annehmen kann, je nachdem wie die Folge aussieht.
x-x geht gegen 0,
x-2x geht gegen -∞
2x-x geht gegen ∞
Obwohl jedesmal die Form "∞-∞" angenommen wird
Alles klar, es wäre unendlich - unendlich Wie kommt man dann auf den Limes?
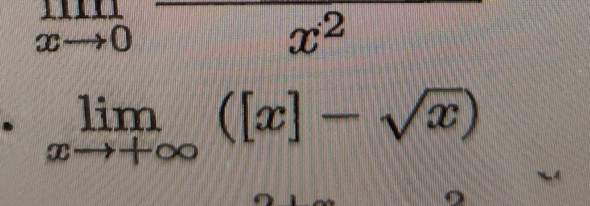
Würde die umreibung nicht Wurzel(X)(Wurzel(X)-1)-1 lauten?