Wie geht diese Aufgabe?



Answer 1

[mihisu]

Beide Seiten der Gleichung bzgl. x ableiten. (Das Nachdifferenzieren von y aufgrund der Kettenregel nicht vergessen.) Dann nach der Ableitung y' auflösen.

Siehe auch: https://de.wikipedia.org/wiki/Implizite_Differentiation

Answer 2

[gauss58]

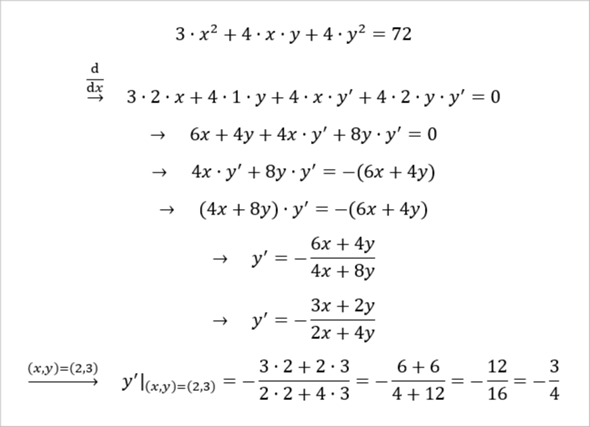
Es handelt sich um eine Ellipsengleichung. Stellt man diese nach y um, so entstehen 2 Funktionszweige:

y1 = (-x/2) + ((√2)/2) * √(36 - x²)

y2 = (-x/2) - ((√2)/2) * √(36 - x²)

Interessant ist nur der erste Funktionszweig, da dieser den Punkt P (2│3) enthält.

Ableitung:

f'(x) = (-1/2) - (x / √(72 - 2x²))

x = 2 einsetzen

f'(2) = -3/4

Answer 3

[jss13]

Du musst die erste Ableitung der Funktion bestimmen und dann den x-Wert einsetzen :)

Comments

[KryptonDB]

Ja aber da sind noch y Werte... Wie kriege ich die weg?

[jss13]

@KryptonDB

Sry, ich hätte die Aufgabe besser richtig angeschaut

Ich würde das in die Form y=... umstellen und dann die Abkeitung usw. berechnen

Answer 4

[Sophonisbe]

Steigung an dieser Stelle berechnen...

Comments

[KryptonDB]

Ja wie?

[Sophonisbe]

@KryptonDB

Ableitung

[KryptonDB]

@Sophonisbe

Ja aber wieach ich dass ich kenne es nur mit einem x aber. Nicht mit 2 parameter... Geht man da genauso vor?

[Sophonisbe]

@KryptonDB

Umstellen. Y = ....

[KryptonDB]

@Sophonisbe

Das. Funktioniert nicht

[Sophonisbe]

@KryptonDB

Das. Funktioniert nicht

Doch.