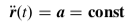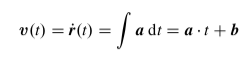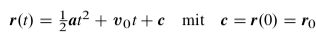Wie erklärt sich das Minus beim Übergang von v(t) zu a(t) durch Ableiten? Was übersehe ich?
v = Weg/Zeit ..... = s/t
d/dt (v(t) wäre doch -1 * s/t^2 ???
Die Beschleunigung a(t) ist die erste Ableitung der Geschwindigkeit v(t)
nach der Zeit t:

7 Antworten
Ganz allgemein gilt:
v = ds/dt
a = dv/dt
Entsprechend folgt über das Integral:
s(t) = s(t0) + int[t0, t]{ v dt}
v(t) = v(t0) + int[t0, t]{ a dt}
Im Falle einer gleichförmig beschleunigten Bewegung (a = const.) folgt:
dv/dt = a = const.
Entsprechend folgt mittels Integral:
v(t) = a*(t - t0) + v(t0)
Und schließlich für die zurückgelegte Strecke:
s(t) = s(t0) + v(t0)*(t - t0) + 0.5*a*(t - t0)^2
Im Falle a = 0 reduziert sich diese Gleichung auf den von dir genannten Spezialfall:
s(t) - s(t0) = v(t0)*(t - t0)
Falls du das reine mathematische ansprichst, erklärt sich das dadurch, dass das t im Nenner steht. s/t ist ja nichts anderes als
Und das ist abgeleitet
was man als
schreiben darf.
Jedoch gibt es hier noch ein ganz anderes Problem. Mathematisch macht das zwar Sinn, aber physikalisch nicht mehr. v=s/t ist ein Spezialfall, der nur dann gilt, wenn es keine a gibt. Die (un)eigentlich richtige Formel ist aber v(t) = v0 + at.
Nur dann ist at = 0*t = 0, ergo also v(t) = v0. Und nur eine v0 darf man als = s/t schreiben.
Leitest du die richtige Formel ab, wäre das: a = v(t) d/(dt) = v0 + at d/(dt) = a
bei der translatorischen (geradlinigen)Bewegung ergeben sich 3 Funktionen (Gleichungen)
1) a=konstant nun 2 mal integrieren
2) V(t)=a*t+Vo hier Vo=Anfangsgeschwindigkeit zum Zeitpunkt t=0
3) S(t)=1/2*a*t²+Vo*t+So hier So=schon zurückgelegter Weg zum Zeitpunkt t=0
Die Integrationskonstanten sind C1=Vo und C2=So
Hinweis:Die Beschleunigung a,die Geschwindigkeit v und der Weg s sind Vektoren,die je nach Aufgabe ein positives oder negatives Vorzeichen haben können.
Standardfall:freier Fall
mit Vo=0 und So=h=Fallhöhe
1) a=-g
2) V(t)=-g*t
3) S(t)=-1/2*g*t²+h
Fallzeit aus 3) S(t)=0=-1/2*g*t²+h
t=+/-Wurzel(h*2/g) mit g=9,81 m/s² die negative zeit fällt weg,weil Unsinn
Aufprallgeschwindigkeit mit 2) V(t)=-g*Wurzel(h*2/g) mit negativen Vorzeichen
Das negative Vorzeichen gibt die Richtung der Geschwindigkeit an,in Richtung nach unten (negative y-Achse)
Hinweis:Bei´m Bremsvorgang ist die Beschleunigung a=negativ,wirkt entgegen der Bewegungsrichtung,die positiv gezählt wird.
Also
ist schon korrekt und da ist auch kein negatives Vorzeichen enthalten!
Dein Fehler liegt darin, dass du eine gleichförmige Bewegung betrachtest, für die
gilt, allerdings gilt bei dieser Form der Bewegung auch a(t) = 0
Korrekt wäre an dieser Stelle für v(t)
Hallo Halbrecht,
für eine gleichförmig beschleunigte Bewegung gilt:
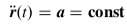
Dann folgt für deine Geschwindigkeit:
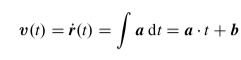
Und dann ist deine Ortskurve offensichtlich:
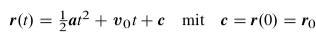
Deine Formel:
gilt nur dann, wenn v(t)=const. ist!! z.B wenn ein Auto eine Strecke von 50km in einer Stunde zurücklegt (v(t)=50km/h).
Und wenn du eine Konstante ableitest kommt Null raus und nicht !!