Wie bestimme ich das Trägheitsmoment?
Guten Abend, ich verstehe nicht wie man auf das Trägheitsmoment eines Körpers kommen soll, wenn die Drehachse senkrecht auf die Körperachse steht.
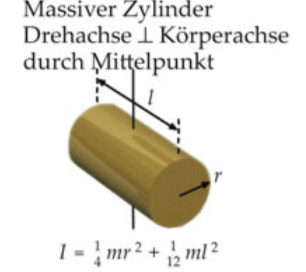
Ich habe mal ein Bild zum Beitrag dazugemacht.
Wenn die Körperachse und die Drehachse gleich sind, kann man es ja ganz leicht in Beispielsweise Zylinderkoordinaten ausrechnen, aber ich habe meine Probleme, wenn die zwei Achsen eben nicht miteinander stimmen und senkrecht aufeinander stehen
Danke für die Antworten
4 Antworten
Du kannst da auch über ein System aus Zylinderkoordinaten integrieren, darfst aber für den Radius über den du integrierst nicht einfach den Radius im Zylinderkoordinatensystem verwenden.
Kleiner Tipp nebenbei: Hättest du in der Vergangenheit "Hilfreichste Antworten" verteilt, dann hätte auch ich mir mit dieser Antwort mehr Mühe gegeben.
Bin was das angeht ein bisschen vergesslich, trotzdem vielen Dank für deine Hilfe und den Tipp
Hättest du in der Vergangenheit "Hilfreichste Antworten" verteilt, dann hätte auch ich mir mit dieser Antwort mehr Mühe gegeben.
Kommt leider sehr oft vor hier. Oft schauen Leute nicht mal mehr auf die Antwort, wenn diese nicht innerhalb von 5min kommt. Manchmal wundert man sich nur noch...
Hier die komplette Ausrechnung auf dem Silbertablett. Sie gelingt am einfachsten in kartesischen Koordinaten. Anfangs hatte ich es über Zylinderkoordinaten versucht. Da geht man unter. In kartesischen Koordinaten ist es verblüffend einfach.

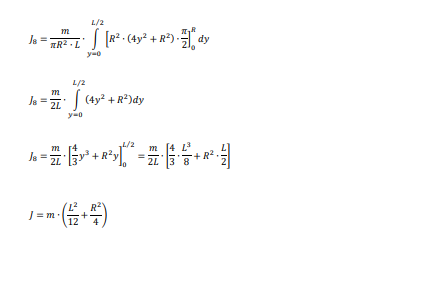

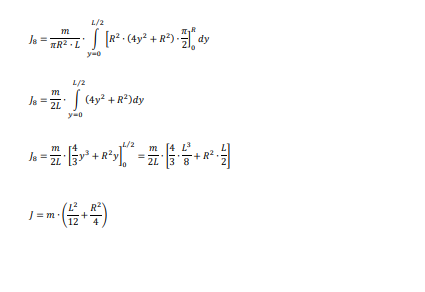
Wow, vielen lieben Dank, dass du dir noch des Wegen die Mühe gemacht hast, jetzt weiß ich endlich wie es geht, danke !
Hier ein paar Kritzeleien, die Dir vielleicht einen Hinweis geben, wie man ein solches Trägheitsmoment ausrechnen kannst. Die Symmetrien erlauben die Berechnung eines Achtelraumsegmentes. Diese muss wegen variabler Integrationsgrenzen in zwei Teilgebiete aufgeteilt werden. Für das schraffierte Gebiet habe ich die Rechnung schon mal angefangen.
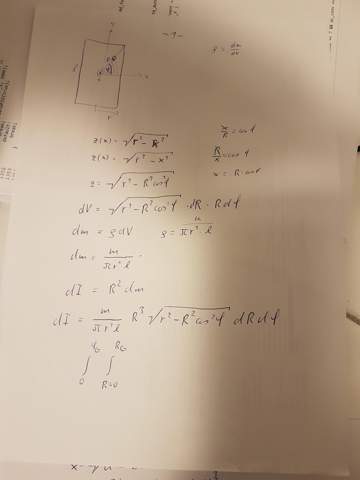
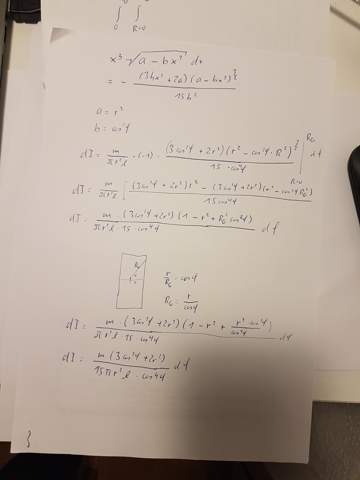
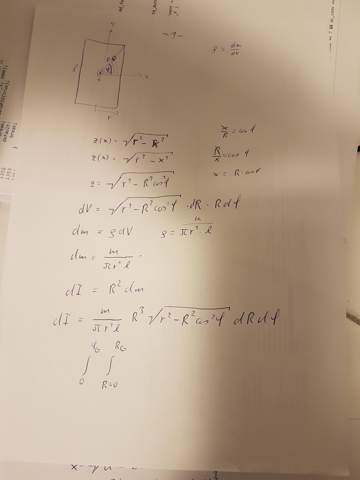
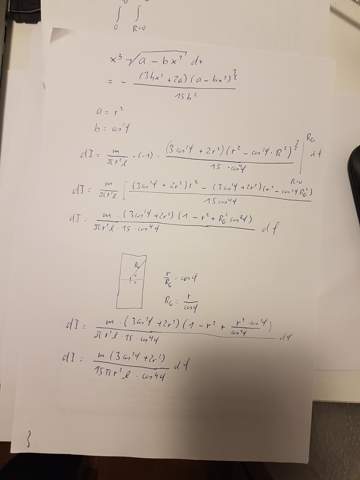
Du denkst dir den Zylinder in lauter kleine Scheiben zerschnitten und integrierst über diese.
Daraus wird bei unendlich vielen Scheiben ein Integral.