Wie berechnet man die Nullstellen von dieser Funktion?

Bin in der 10. und man kann dabei ja keine P-Q-Formel oder sonstiges anwenden, weshalb ich mich frage, wie man die Nullstellen davon berechnet.
2 Antworten
Hallo,
raten und Polynomdivision kannst Du hier vergessen.
Die drei Lösungen lauten x1=0,9032119259, x2=-3,709275359, x3=-1,193936566.
Wenn Du die cardanische Formel nicht beherrschst (tun Schüler normalerweise nicht), bleibt Dir nur das Newton-Verfahren oder ein anderes Näherungsverfahren, welche aber jeweils nur eine Nullstelle liefern und bei denen man nicht sehen kann, ob es noch mehrere gibt. Das einfachste: Schnapp Dir den Taschenrechner, ruf das Programm für das Lösen von Polynomgleichungen auf und laß den ran.
Wer Schülern so eine bescheuerte Aufgabe stellt, hat's nicht besser verdient.
Herzliche Grüße,
Willy
Am einfachsten ist eine graphische Lösung z.B. mit einem Funktionenplotter:
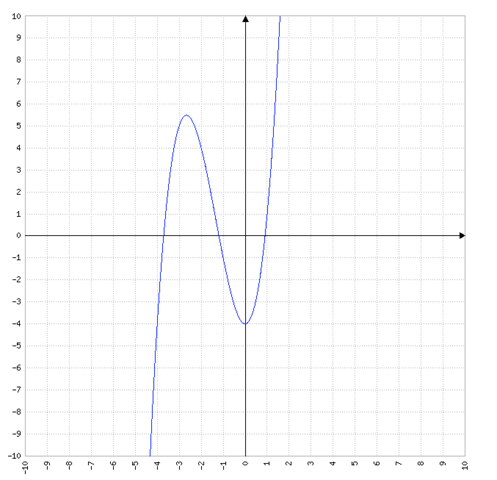
Die einzelnen Nullstellen kann man durch eine höhere Auflösung präzisieren wie z.B. so:


