Wenn 2 Lichtsignale sich mit Lichtgeschwindigkeit aufeinander zu bewegen. Wie schnell bewegen sie sich relativ zueinander?
Wenn 2 Lichtsignale sich mit Lichtgeschwindigkeit aufeinander zu bewegen. Wie schnell bewegen sie sich relativ zueinander?
Beispiel 1:
Planet A ist zu Planet B 1 Lichtjahr entfernt und Planet B ist zu Planet C auch 1 Lichtjahr entfernt.
A----1lj----B----1lj----C
Alle 3 Planeten stehen auf einer Linie.
Planet A und C sind zueinander 2 Lichtjahre entfernt.
A und C schicken gleichzeitig einen Lichtsignal auf den in der Mitte befinden Planeten B.
Wie schnell haben sich die Lichtsignale A und C relativ zueinander bewegt?
Wann kommen die Lichtsignale auf Planet B an?
Wie viel Zeit ist auf Planet B vergangen?
1 Jahr? Mehr oder weniger?
Das gleiche wollen wir mit zwei Körpern machen.
Beispiel 2:
Zwei bemannte Raketen starten gleichzeitig mit annähernder Lichtgeschwindigkeit von A und C richtung B.
Wie schnell waren A und C relativ zueinander?
Wann kommen die Personen auf Planet B an?
Wieviel Zeit ist auf Planet B vergangen?
1 Jahr? Mehr oder weniger?
Gab es eine Zeitdilatation?
Person A und C waren vor dem Start im gleichen Alter.
4 Antworten
Man wendet das Theorem der Addition von Geschwindigkeiten an.
Um die Unbestimmtheit aufzuheben, berechnen wir ein Limes folgendermaßen:
Die Photonen bewegen sich also mit Lichtgeschwindigkeit c voneinander.
Herzliche Grüße,
arhimedes
Das kann man so schlecht sagen, weil eine Geschwindigkeit relativ zu einem Teilchen ja eigentlich die Geschwindigkeit im Ruhesystem des Teilchens bedeutet, und Photonen gar kein Ruhesystem haben.
Hallo cemo111,
die Frage ist interessant und hat eine überraschende Anwort: Die Relativgeschwindigkeit zwischen zwei Lichtsignalen ist gar nicht definiert. Genauer gesagt, eine Geschwindigkeit relativ zu einem Lichtsignal ist nicht definiert.
Mit der Relativgeschwindigkeit v› eines Punkt oder Objekt O’ relativ zu einem anderen Punkt oder Objekt O ist die Geschwindigkeit von O’ mit O als Bezugspunkt bzw. Bezugsobjekt gemeint, und ein Bezugspunkt für Positionen oder Geschwindigkeiten gilt dabei als ruhend, also v›_[O]=0.
Dann und nur dann, bzw., wenn |v›_[O]|≪c (c ist der Betrag der Lichtgeschwindigkeit) ist, ist die Relativgeschwindigkeit näherungsweise gleich der Differenzgeschwindigkeit, also
v› ≈ v›_[O’] – v›_[O],
andernfalls ist
|v›| < |v›_[O’] – v›_[O]|.
Der Grund dafür ist zweierlei:
- GALILEIs Relativitätsprinzip (RP): Die grundlegenden Beziehungen zwischen physikalischen Größen (Naturgesetze) hängen nicht von der Wahl des Bezugspunktes ab. Man kann also O als ruhend und O’ als mit v› bewegt, aber auch O’ als ruhend und O als mit –v› bewegt ansehen.
- MAXWELLs Elektrodynamik: Sie gehört natürlich auch zu den Naturgesetzen und müssen von der Wahl des Bezugspunktes unabhängig sein - samt allem, was direkt daraus folgt. Darunter ist auch, dass sich elektromagnetische Wellen im materiefreien Raum mit c ausbreiten.
Zu MAXWELLs Zeiten und auch später wurde das RP in Frage gestellt, da man an eine Supersubstanz namens Weltäther als Ausbreitungsmedium glaubte, sodass man Bewegung relativ zu diesem eindeutig müsse ausmachen können. MICHELSON und MORLEY versuchten dies in einem Experiment (kurz MMX), aber ohne Erfolg, obwohl sich die Erde in einem an die Sonne gekoppelten Inertialsystem (Koordinatensystem, das keinen Kräften unterliegt) immerhin mit ca. 10⁻⁴c um die Sonne bewegt.
Der negative Ausgang des MMX veranlasste LORENTZ et al. zur Aufstellung von Gleichungen zur Umrechnung (Transformation) zwischen den Interpretationen von O als ruhend und O’ als ruhend, aber noch als Äthertheorie und einer Unterscheidung zwischen „Ortszeit“ und der „eigentlichen Zeit“.
Relativität der GleichzeitigkeitErst EINSTEIN berief sich 1905 nur noch auf GALILEI und wandte ihn einfach auf MAXWELL an. Natürlich sind die von ihm verwendeten Transformationen mit den LORENTZ-Transformationen identisch, denn die waren ja auch an eine fehlende Abweichung vom RP angepasst.
Kernstück von EINSTEINs Überlegungen ist dabei die Absolutheit von c (das da irrtümlich als zusätzliche Forderung auftaucht) und die daraus folgende Relativität der Gleichzeitigkeit (RDGz) zweier räumlich getrennter Ereignisse.
Dass die „Gleichortigkeit“ zeitlich aufeinander folgender Ereignisse schon nach GALILEI/NEWTON relativ ist, also davon abhängt, ob etwa O oder O’ als ruhend gilt, wird schnell klar, wenn man mal darüber nachdenkt: Ich sitze in einem Café; irgendwann zwischendurch fährt ein Zug mit 60m/s an mir vorbei. Ich trinke in 5 Minuten einen Kaffee. Den ersten und letzten Schluck nehme ich am selben Ort ein - wenn ich mich als ruhend betrachte. Ich kann aber auch die Erde als riesiges Laufband betrachten, auf dem der Zug auf der Stelle rollt, und demnach liegen diese beiden Schlucke nicht nur 300s, sondern auch 18km auseinander.
Wenn nun bei x=–3km und x=+3km (x=0 Café, x Fahrtrichtung des Zuges) ein Blitzlicht aufleuchtet und ich sie gleichzeitig sehe, werde ich sie auch als gleichzeitig deuten, wenn ich das Café als ruhend ansehe. Sehe ich es und damit auch die Lichter als bewegt an, muss ich dagegen davon ausgehen, dass das bei x=+3km liegende Licht dem Punkt, wo ich jetzt bin, näher kommt und beim Aufleuchten weiter weg war als das bei x=–3km liegende Licht (lächerlich wenig, aber das soll uns nicht stören).
In dieser Interpretation muss das Licht bei +3km also eine winzige Zeitspanne früher aufgeleuchtet haben als das bei –3km, damit ich sie an Ort und Stelle gleichzeitig sehen kann.
Die sogenannten „relativistischen Effekte“ wie „Zeitdilatation“ und „Längenkontraktion“ (die LORENTZ zuerst ins Spiel gebracht hatte) sind nur Nebeneffekte der RDGz.
MINKOWSKIs RaumzeitEs ist immer sinnvoll, Zeit und Raum kurzerhand zur Raumzeit zusammenzufassen. Wenn Du ein Date hast, musst Du ja auch Ort und Zeit angeben. EINSTEINs Betrachtungen machen diese Zusammenfassung jedoch unerlässlich, denn nicht nur der Raum lässt sich von der Zeit nicht trennen (das war schon bei GALILEI/MAXWELL so), sondern auch umgekehrt.
Räumliche Abstände, etwa in einer Ebene mit „längs“ (1z›) und „quer“ (1x›) als Richtungen, folgen dem Satz des Pythagoras,
(1) Δs² = Δz² + Δx² ≡ Δz°² + Δx°²,
wobei Δz° und Δx° Längs- und Querabstand in einem relativ zum ursprünglichen gedrehten Koordinatensystem sind. Raumzeitliche Abstände nach EINSTEINs Lehrer MINKOWSKI sind hingegen durch
(3.1) Δt² – Δs²/c² ≡ Δt’² – Δs’²/c² =: Δτ²
bzw.
(3.2) Δs² – c²Δt² ≡ Δs’² – c²Δt’² =: Δς²
gegeben. Sie sind absolut und für Photonen gleich 0.
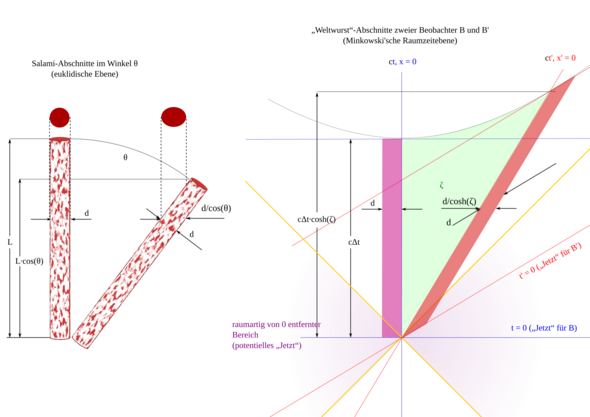
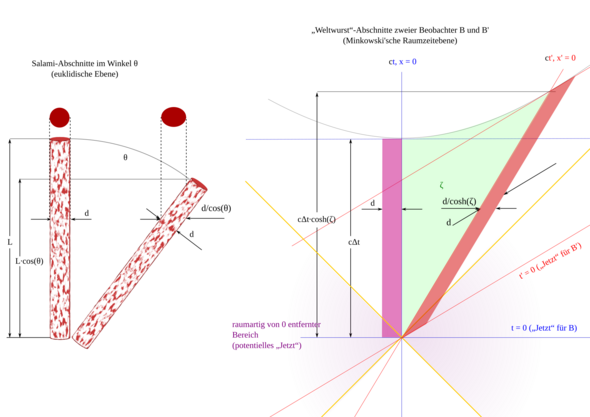
Eine LORENTZ-Transformation ist mithin eine Art Drehung in der Raumzeit, genauer eine hyperbolische Drehung. O’ erlebt nicht schlechthin weniger Zeit als O, „weil er sich bewegt“, sondern nur quasi längs zur Zeitrichtung von O, und vice versa. Das Wort „Zeitdilatation“ ist daher mehr als irreführend und auch „Längenkontraktion“. Kein Mensch käme auf die Idee, einen Schrägschnitt durch eine Salami „Breitendilatation“ zu nennen.
zu 1. die lichtgeschwindigkeit ist absolut also treffen beide signale nach einem jahr bei B ein.
zu 2. bei dem beispiel musst fu die zeitdilatation mit dem lorentzfaktor einbrechnen.
Wenn die Photonen sich relativ zueinander bewegen, ist die Sache einfacher.