Wendepunkt mit höheren Exponenten berechnen?
Hallo Leute
ich sitze verzweifelt an meinen Mathe Hausaufgaben und komme einfach nicht weiter... Hab gegoogelt und auf YouTube geschaut, aber nichts erklärt es wie ich die Aufgabe habe.
Meine Funktion lautet :
f(x) = x^4 - 3x^2 + 3
Mein Problem bildet sich in der Notwendigen Bedingung, und zwar wird ja die 2.Ableitung gleich 0 gesetzt.
f”(x) = 0
12x^2 - 6 = 0 | +6
12x^2 = 6 | :12
x^2 = 0,5
Und da ist auch schon das Problem.
Dieses x^2 , muss ja zu einem x werden.
Ich dachte zuerst ich muss die Wurzel ziehen von 0,5 , hab dann aber auf YouTube bei TheSimpleClub gesehen das die das auf 2 Lösungen geteilt haben. Also bei denen kam in der Aufgabe sah das am Ende so aus :
:
:
x^2 = 1
x1 -> 1 , x2 -> -1
Das hat mich unheimlich verwirrt, woher kommt bitte die -1? Und ich brauche doch nur eine Zahl damit ich die einsetzen kann für die 3.Anleitung also die Hinreichende Bedingung.
Und in Aufgabe 2 ist sogar die Funktion :
f(x) = 0,05x^5 - 0,25x^4 - 0,35x^3 + 2,05x^2 - 1,5x
ich komme mit diesen höheren Exponenten nicht zurecht , ich weiß nicht wie ich das lösen soll. Ich tu euch mal ein Bild rein, damit ihr seht wie ich es gemacht habe, ich weiß das es falsch ist aber damit ihr das vielleicht besser nachvollziehen könnt.
Bitte wenn ihr antwortet nutzt nicht soviel Fachbegriffe, damit ist mir auch nicht wirklich geholfen, ich brauche das einfach einmal vernünftig erklärt, was bei den Lehrern im Homeschooling zu wünschen bleibt.
schreibe bald die Klausur , also bitte helft mir :(

3 Antworten
f(x) = 0,05x^5 - 0,25x^4 - 0,35x^3 + 2,05x^2 - 1,5x
f'(x) = 0,25x^4 - x^3 - 1,05 x^2 + 4,1x - 1,5
f''(x) = x^3 - 3x^2 - 2,1x + 4,1
f'''(x) = 3x^2 - 6x - 2,1
Notwendige Bedingung:
f''(x) = 0
x^3 - 3x^2 - 2,1x + 4,1 = 0
Dasist jetzt nich so ganz einfach, die Nulstellen einer Gleichung dritten Grades zu finden, das es dafür keinen Algorithmus gibt. Da bleibt nichts anderes übrig, als eine Nullstelle zu raten und dann durch Polynomdivision das ganze auf eine quadratische Gleichung zu reduzieren. Ein anderes Verfahren wäre, sich die Funktionmit einem Funktionsplotter zeichnen zu lassen und eine Nullstellle abzulesen.
Meistens liegt mindestens eine Nullstelle im Bereich von -1 bis +1. Der Abschnitt
- 2,1x + 4,1 gibt durch die 1 hinterm Komma einen Hinweis. Die kriegt man nur weg, wenn x = 1 ist, denn dann fällt bei 4,1 - 1 * 2,1 die Zahl hinterm Komma weg. Alsoporbieren wir mal 1 aus und stellen fest:
1 - 3 - 2,1 + 4,1 = 0
Damit wäre eine Nulllstelle gefunden. Mit dem Funktionsplotter kommen wir auch auf die 1:
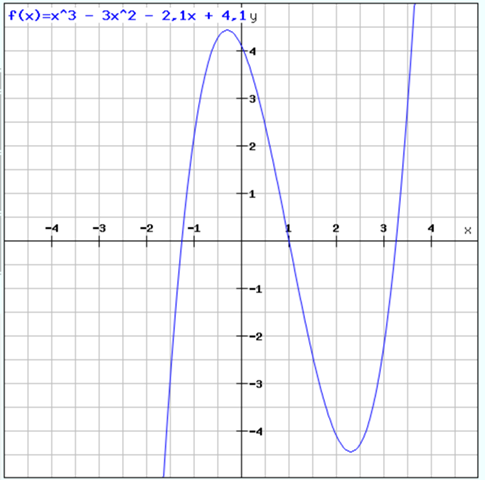
Nun führen wir eine Polynomdivision durch:
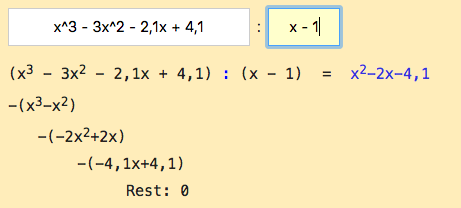
Für die quadratische Gleichung
x^2 - 2x - 4,1 = 0
können wir die pq-Formel anwenden:

Nun haben wir die 3 möglichen Wendestellen gefunden:
x1 = -1,258
x2 = 1
x3 = 3,258
Wie es weitergeht, weißt du ja. Du musst jetzt alle drei Lösungen weiter mit f''' untersuchen bzw. den Funktionswert f(x) berechnen.
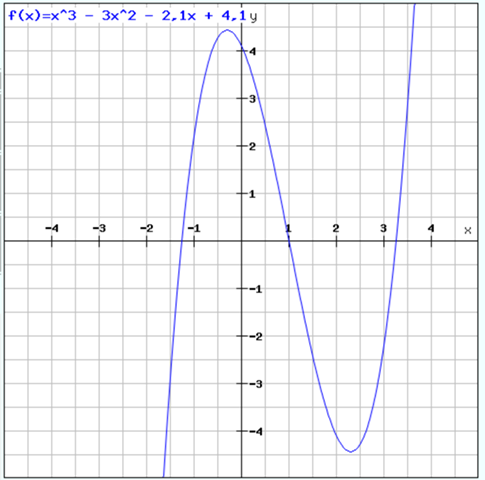
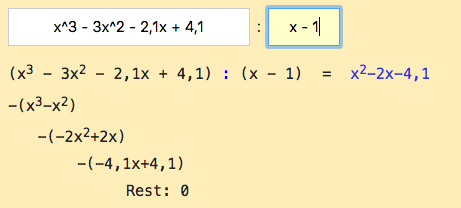

Du hast
x^2 = 0.5
Da hast du zwei Lösungen,
+- sqrt (0.5)
Hallo , hab’s grad hinbekommen. Sitze jetzt allerdings an Aufgabe 2, die 3mal so schwer ist. Ich würd mich freuen wenn du mir bei Aufg. 2 weiterhelfen könntest die Notwendige Bedingung rauszubekommen.
Du möchtest jetzt nur die Wendestelle ausrechnen oder ?
Hallo , hab’s grad hinbekommen. Sitze jetzt allerdings an Aufgabe 2, die 3mal so schwer ist. Ich würd mich freuen wenn du mir bei Aufg. 2 weiterhelfen könntest die Notwendige Bedingung rauszubekommen.