Größte Wachstumsgeschwindigkeit?
Ich lerne gerade für Mathe und hänge an der Aufgabe ''Zu welchem Zeitpunkt ist die Wachstumsgeschwindigkeit am größten?'' fest. Die Funktion dazu lautet: f(x)= -0,005x^3+0,25x^2+0,5x
Wäre dankbar, wenn mir jemand sagen könnte, was ich rechnen muss, oder zumindest wie ich anfangen muss :/
3 Antworten
Ich gehe mal davon aus, dass Deine Funktion einen Bestand zu einem Zeitpunkt x wiedergibt (nicht das Wachstum eines Bestandes).
Dann berechnest Du mit der ersten Ableitung das Wachstum. Von diesem wiederum ist ein Maximum gesucht. Also brauchst Du einen Hochpunkt von f´. Dieser entspricht einem Wendepunkt Deiner Originalfunktion mit positiver Steigung.
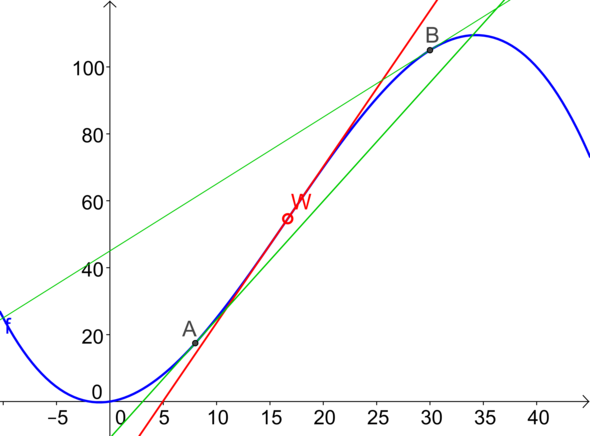
Ich füge mal ein Bild Deiner Funktion bei. Darin habe ich die Tangente im Wendepunkt und zwei weitere Tangenten eingezeichnet. Man sieht (hoffentlich) deutlich, dass die Tangente in W die größte Steigung hat - und danach ist gesucht.
tooob93 und lordkopf suchen nach Extrema von f, das wäre also der höchste Bestand, nicht das größte Wachstum.
Wird dagegen mit f ein Wachstum zu einem Zeitpunkt x beschrieben, dann wäre deren Ansatz richtig.
Also die extremstellen dann rechnen, wenn Die Zeit gefragt ist, also x. Den Wendepunkt bei Wachstumsgescheindigkeit, wenn y gefragt ist?
du bildest die erste Ableitung und setzt diese gleich null, rechnest den/die x werte davon aus und bekommst dann 1 oder 2 werte heraus
wenn du einen wert herausbekommst, dann hast du dein lokales maxima, bekommst du 2 werte raus, dann musst du noch einmal ableiten und die x werte einsetzen, ist der y wert größer als 0, so hast du ein mimima, ist der y-wert kleiner als 0, dann hast du dein maxima.
nun jedoch musst du noch plus und minus unendlich für x in der normalen funktion einsetzen um zu schauen, ob dort die funktion einen höheren Wert hat.
Viel Erfolg
Die Wachstumsgeschwindigkeit bekommst du erstmal wenn du die Fkt. ableitest (hoffe du weißt wie das geht ansonsten geb ciha uch dazu antwort^_^). Dann setzt du die Fkt. gleich Null und dann musst du gucken welcher Wert am größten ist(am positivsten, sofern du mehrere ergebnisse hast) und der Wert ist dann der zeitpunkt der größten Wachstumsgeschwindigkeit :) Rechtschriebfehler dürfen behalten werden :)