Was ist der Inhalt der gefärbten Fläche (berechnen)?
Guten Abend,
ich habe es berechnet und es kam genau 5 heraus, kann jemand das kontrollieren?
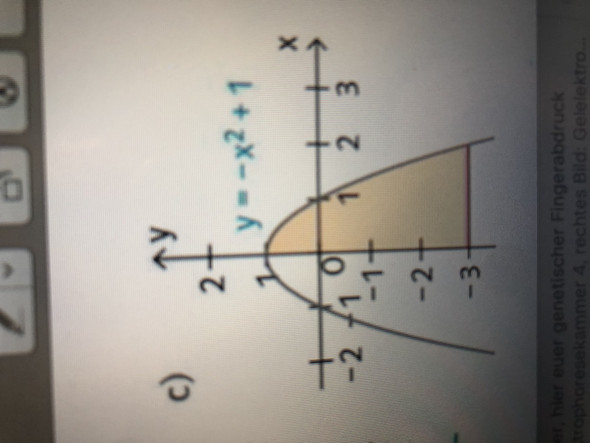
Funktion: y=x^2+1
4 Antworten
Die Gesamtfläche kannst du hier aus 3 Teilflächen berechnen
f(x)=-1*x²+1 Nullstellen 0=-1*x²+1 x1,2=+/- Wurzel(1)=+/- 1
A1=Integral((-1*x²+1)*dx)=-1/3*x³+x+C
A1=obere Grenze minus untere Grenze x0=1 und xu=0
A1=(-1/3*1³+1)-(-1/3*0³+0)=2/3 FE
A2=-3* 2=-6 FE also Betrag A2=6 FE xo=2 ist die Schniitstelle von f(x)=-3
A3=Integral (f(x)*dx) obere Grenze xo=2 und untere Grenze xu=1
A3=(-1/3*2³+2)-(-1/3*1³+1)=(-8/3+6/3)-(-1/3+3/3)=-4/3 FE
A3=Betrag 4/3 FE
Gesamtfläche A=A1+A2-A3=2/3+6-4/3=-2/3+6=5 1/3 FE
A=5 1/3 FE
Wir haben hier eine Fläche zwischen 2 Funktionen
Formel ist A=Integral(f(x)-g(x)
f(x)=-1*x²+1 ist die obere Begrenzung
g(x)=-3 ist die untere Begrenzung
A=Integral((-1*x²+1)-(-3))*dx=Integral((-1*x²+1+3)*dx=Int.(-1*x²+4)*dx
A=-1*Integral(x²*dx)+4*Integral(dx)
A=-1/3*x³+4*x+C
Fläche ist A=obere Grenze minus untere Grenze xu=0 xo=2
f(x)=g(x) -1*x²+1=-3 x1,2=+/- Wurzel((-3-1)/(-1))=+/- 2 ergibt xo=2
A=(-1/3*2^3+4*2)-(-1/3*0³+4*0)=5,33 FE
A=5,33 FE (Flächeneinheiten)
5 1/3 sollte rauskommen nach meiner Rechnung...
Die gefärbte Fläche geht von x=0 bis x=2. Zuerst verschiebst Du den Graphen um 3 Einheiten nach oben, damit die Fläche mit der x-Achse abschließt. Die verschobene Funktion lautet f(x)=-x²+4. Das jetzt integrieren in den Grenzen von 0 bis 2 und es kommt 5 1/3 raus.
Hallo,
ja das sollte passen
Die Stammfunktion berechnet sich wie gewohnt mit der Potenzregel
F(x) = -1/3 x^3 + x + c
g(x)= -3
Da du aber die Fläche zwischen zwei Graphen berechnest, musst du folgendes tun:
Als erstes die Schnittpunkte der Funktionen bestimmen, die kann man hier aber auch direkt ablesen. x= -2 und x=2
Da du jetzt aber nur die Hälfte der Fläche zwischen den zwei Graphen benötigst gilt folgendes:
g(x)= -3
Integral von 0 bis 2 von f(x)-g(x) dx
= Integral x^2 + 1 - (-3) = Integral x^2 +4 dx = [-1/3 x^3 + 4x] von 0 bis 2
--> Bestimmtes Integral berechen:
-8/3 + 8 = -8/3 + 24/3 = 16/3 ≈ 5,33
Kannst du mir mal die Stammfunktion von der oberen Funktion sagen
ich verstehe nämlich nicht wie genau die zustande kommt