Warum ist eigentlich cos(x) = sin(x+ pi/2)?
Hallo
meine Frage lautet warum die Verschiebungsformel so ist wie sie ist ?
Würde mich auf vernünftige Antworten freuen :)
3 Antworten
Beide haben grundsätzlich die selbe Kurve (Welle), allerdings "startet" Cosinus bei 1 und Sinus bei 0. Sinus erreicht 1 bei 90°, während Cosinus dann runter auf 0 ist. Im Grunde hast du also 2 Kurven die identisch, aber verschoben sind.
360° entspricht 2*pi, also sind pi/2 entsprechend 90°.
Wenn du bei Sinus also noch die 90° hinzufügst, laufen beide Wellen im Einklang. Daher:
cos(0) = sin(0+90)
cos(x) = sin(x+90)
cos(x) = sin(x+pi/2)
Gut zu sehen bei dieser Grafik:
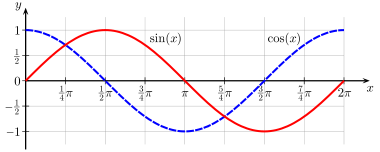
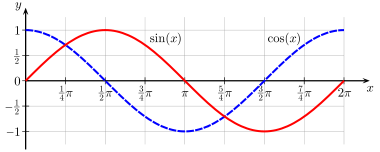
Das sieht man ein, wenn man sich die Definition am Einheitskreis anschaut.
https://www.matheretter.de/wiki/einheitskreis-sinus-kosinus
https://www.mathe-online.at/lernpfade/einheitskreis/?kapitel=2
Aus der Symmetrie folgt dann sofort die Beziehung:
cos(x) = sin(x + pi/2)
Sieh dir die Graphen von Sinus und Cosinus an. Wenn du den vom Sinus um pi/2 nach links verschiebst, hast du genau den Cosinus