Wahrscheinlichkeiten addieren?
Die Wahrscheinlichkeit blaue Haare zu haben liegt bei 41%. Drei Menschen kommen in einen Raum, wie hoch ist die Wahrscheinlichkeit, dass mindestens einer blaue Haare hat? Ich dachte, man muss die Wahrscheinlichkeiten addieren, also drei mal 41%, aber 123% kann ja nicht richtig sein, oder?
5 Antworten
Hallo,
ist genau einer gemeint, also nicht zwei oder alle drei?
Addieren ist schon richtig - aber Du darfst nicht das Falsche addieren.
41 % ist die Wahrscheinlichkeit dafür, daß ein Mensch, der in den Raum kommt, blaue Haare hat
Bei drei Menschen mußt Du drei Fälle betrachten und deren Wahrscheinlichkeiten addieren, wenn nur einer von ihnen blaue Haare haben soll:
Fall a) Der Erste hat blaues Haar. Dann müssen die beiden anderen eine andere Haarfarbe haben.
Du rechnest also 0,41*0,59*0,59, denn wenn die Wahrscheinlichkeit für blaues Haar 41 % beträgt, dann ist die Wahrscheinlichkeit für eine andere Haarfarbe (oder Glatze) natürlich 100 %-41 %=59 %.
Wenn der Zweite blaues Haar hat, ist es 0,59*0,41*0,59 und beim Dritten:
0,59*0,59*0,41.
Da es bei einer Multiplikation nicht darauf ankommt, in welcher Reihenfolge multipliziert wird, haben alle drei Fälle die gleiche Wahrscheinlichkeit und Du rechnest einfach 3*0,41*0,59²=0,428163 oder etwa 42,8 %.
Geht es darum, daß mindestens einer von den Dreien blaues Haar hat, ziehst Du die Wahrscheinlichkeit dafür, daß niemand blaues Haar hat, von 1 ab, denn in allen anderen Fällen taucht mindestens einer mit blauem Haar auf:
1-0,59³=0,794621 oder etwa 79,46 %.
Herzliche Grüße,
Willy
Also, du rechnest nicht 41 plus 41 plus 41...sondern mal. Aber nicht 41 * 41 * 41, sondern 0.41 * 0.41 * 0.41, weil du sonst den 1.00 vollen faktor mit behälst, was dann in einer definitiven wahrscheinlichkeit endet.
0.41 * 0.41 * 0.41 = 0.068, also eine 6.8% Wahrscheinlichkeit das alle drei blaue haare hätten.
Wenn du extra nur fragst wie hoch die wahrscheinlichkeit ist das EINER blaue haare hat, dann brauchst du die wahrscheinlichkeit generell das es einer hat von 3, also 1/3, und das mal 0.41
0.33 * 0.41 = 0.13, also eine 13% Chance das einer blaue haare hat von denen
Ist ja auch so
Je mehr Leute es gibt; desto mehr Möglichkeiten du hast umso niedriger die Wahrscheinlichkeit
Natürlich nicht. Wenn viele Leute den Raum betreten, ist die Wahrscheinlichkeit mindestens jemanden mit einem Merkmal X zu finden natürlich grösser als davor.
Es kommt darauf an ob du fragst das nur EINER blaue haare hat, aber sonst keiner, oder EINER ODER MEHR, also MINDESTENS EINER.
Wenn dann müsste man muss es multiplizieren
Hier geht man aber über das Gegenereignis, das heißt, das keiner Blaue Haare hat.
Wahrscheinlichkeit keine Blaue Haare: 0,59/ 59%
Wahrscheinlichkeit:
P= 1-Gegenereignis
P=1-0,59*0,59*0,59
P=1-0.205
P=0,795 = 79,5%
Ich musste tatsächlich kurz überlegen hahaha.
Hier liegt eine Binominalverteilung vor mit:
(Falls du GENAU einen meinst)
Wenn du MINDESTENS einen meinst dann ist
----
Hier der Plot
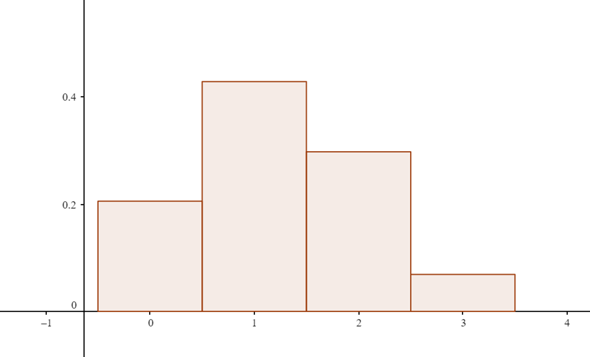
Im ersten Fall liegt die Wahrscheinlichkeit bei etwa 42.8%
Im zweiten Fall liegt sie bei etwa 79.4%
;) Perfekt, ich hätte dir aber um ehrlich zu sein nicht genau sagen können, was falsch war. Ich wusste nur, dass es das war. Aber jetzt wo du es sagst, macht es Sinn!
man muss ja jede "person" einzeln sehen also jede kann einen anderen "wert" annehmen so ist es richtig :)
Die Wahrscheinlichkeit, keine blauen Haare zu haben, liegt bei 0,59. (Lass bitte die Prozentrechnung raus, das ist nur was für Pauker und ihre Zöglinge.)
Die Wahrscheinlichkeit, dass alle 3 keine blauen Haare haben, liegt bei 0,59^3=0,205.
Also liegt die Chance, dass einer von denen blaue Haare hat, bei 0,795.
Das ist nicht richtig. Das würde ja bedeuten, die Wahrscheinlichkeit nimmt ab, je mehr Leute den Raum betreten ?