Thema 'Optimierung' ( Mathe, 10.Klasse Gymnasium) ?
Hallo, könnte mir jemand das Thema Optimierung in Mathe so einfach wie möglich erklären? Danke schonmal im voraus. 😊
3 Antworten
Das Stichwort "Extremstellen" ist schon gut; genau die Methode ist gefragt.
Dazu benötigst Du eine Funktion, die Du auf Extremstellen (in diesem Fall: auf eine Maximumstelle) untersuchen sollst.
Hauptbedingung: Die Fläche des Rechtecks soll maximal werden.
Erst mal: Skizze machen! Alles, was Du weißt, kennzeichnen. Was ist gesucht?
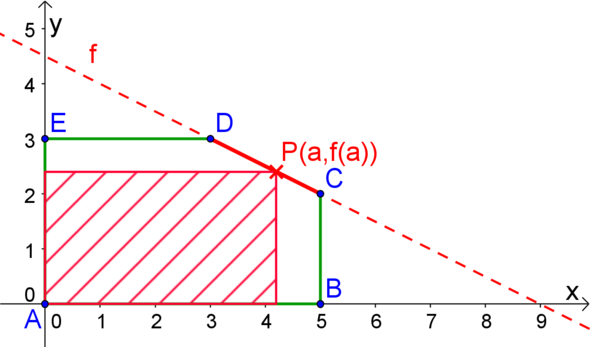
Ich habe mal eine Skizze gefertigt und gehe davon aus, dass man den Punkt "rechts oben" der neuen Scheibe sucht.
In diesem konkreten Fall würde ich Dir raten, die "schräge" Seite durch eine Funktion f zu beschreiben (mit den Punkten C und D). (weil Du es häufiger mit Problemen zu tun hast, bei denen ein Punkt eines Rechtecks... auf dem Graphen einer Funktion liegt)
Dann hat das gesuchte Rechteck den Flächeninhalt A(a) = a · f(a).
Auf diese Funktion A wendest Du nun Deine Kenntnisse zur Bestimmung von Extrema an.
Und schon ist das Problem gelöst :-)
Meinst du "Extremwertaufgaben" ?
Oft wirt nach der maximalen Fläche eines Rechtecks unter einer Funktion gefragt.Kann sein,dass nur eine Zeichnung gegeben ist.Man muss dann aus der Zeichnung die Funktion f(x) erst ermitteln.
Rechteckfläche Ar= a *b= y * x=f(x) * x
Ar= a*b hat 2 Unbekannte Mit f(x) eingesetzt,ergibt sich eine Funktion wie y=f(x)
Hier dann Ar(x) =....
Der Rest ist dann nur noch eine einfache Kurvendiskussion.Ableiten und Extremstellen bestimmen.
Optimierung von was?
Generell ist eine Optimierung die Verbesserung eines Zustandes bis zum für den jeweiligen Nutzer bestmöglichen Ergebnis.
Welches Thema behandelt Ihr grad in Mathe?
Da könnte das hier helfen: http://mathebibel.de/lineare-optimierung
Gibt aber natürlich auch nicht-lineare Optimierung (;
Dann ist die "Optimierung" wohl das Auffinden von Extremwerten wie Maximum oder Minimum.
Das findest durch Ableitung.
Optimierung zB von einer Fensterscheibe, wo ein Stück Glas abgesprungen ist oben in der Ecke & man soll eine möglichst große Fläche wieder daraus machen also halt ein Rechteck wieder. & ja das mit dem bestmöglichen Ergebnis stimmt :-) Das Thema heißt bei uns Optimierung 😅 Vorher hatte ich etwas mit Extrempunkten, Wendepunkten usw. & dieses Thema soll wohl eigentlich fast das gleiche sein. :-)