Tangente im Punkt P berechnen - ist das so korrekt?
Hallo, ich frage nur, damit ich mir das nun nicht falsch merke. Habe von Aufgaben dieser Art noch knapp 30 vor mir, um mir den rechenweg für immer und ewig merken zu können 😅
nicht dass ich mir nun etwas Falsches merke :)
2 . Und wenn nun der y Wert nicht richtig gegeben wäre und es heißen würde
P(1|f(1)) müsste ich ja lediglich noch den y wert errechnen oder?, was dann von der Art gleich wäre, wie als wenn nur x gegeben wäre???🙈
3 . Warum kann ich hier nicht die Formel
yT= f‘(xB) * (x-xB) + f(xB) anwenden? Die funktioniert ja irgendwie nur bei Fernpunkten, aber warum?
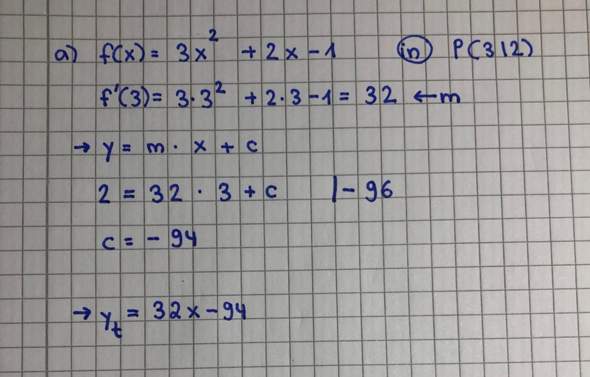
Wäre mega wenn mir jemand kurz helfen könnte :) dankeeee:)
3 Antworten
siehe Mathe-Formelbuch,was du dir privat in jedem Buchladen besorgen kannst.
Kapitel, Differentialgeometrie
Tangentengleichung yt=ft(x)=f´(xo)*(x-xo)+f(xo)
Normalengleichung yn=fn(x)=-1/f´(xo)*(x-xo)+f(xo)
Es gibt 2 Fälle:
1) die Stelle "xo" ist gegeben,wo die Tangente/Normale an der Funktion f(x)=.. liegen soll.
1 Schritt: die Funktion f(x)=... ableiten,dass ergibt f´(x)=..
2 Schritt: den Wert xo in f(xo)=.. und f´(xo)=... errechnen
3 Schritt: die Werte f(xo)=.. und f´(xo)=.. indie Formel einsetzen und ausrechnen
2) ein Punkt P1(x1/y1) ist gegeben und die Funktion f(x)=..,wo die Tangente/Normale durchgehen soll.
1 Schritt: die Funktion f(x)=... ableiten,ergibt f´(x)=...
2 Schritt: Den Punkt P1(x1/y2) in die Formel yt=ft(x1)=y1=f´(xo)*(x1-xo)+f(xo) einsetzen
3 Schritt: nach der Unbekannten xo umstellen und ausrechnen.
Hinweis: Bei diesen Aufgabentyp braucht man nur die 2 Formeln Tangentengleichung oder Normalengleichung
Hinweis:Die ganzen Formeln merkt man sich nicht (es sei denn,es wird von der Schule gefordert,für die Arbeit),man schreibt sich ab und übernimmt sie in eine Formelsammlung,wo sie immer "griffbereit" vorliegen,fals sie benötigt werden.
Merke:"Kopieren geht über studieren ! Man muß nur wissen,wo es steht und man muß damit umgehen können !"
Du musst erst die erste Ableitung nehmen also
f‘(x)=6x+2
dann erst einsetzen
f‘(3)=6•3+2
m=20
wie es weiter geht weißt du ja :)
Ja hab ich irgendwie verpennt...:/ ärgerlich... wie sieht es danach aus? Also angenommen ich hätte es nun abgeleitet und hätte halt 32 rausbekommen, wäre es dann richtig?
Ja aber es kommt 20 raus, du kannst nicht mit 32 weiterrrechnem
Ja ich weis ^^ aber die folgenden Rechenschritte wären richtig gewesen ? Wenn jetzt die Ableitung stimmen würde?
Ja wenn du m,x,y in die Tangentenformen machst kannst du nach c auflösen.Ich hab bei c=-58 wenn ich mich nicht irre.
Dann lautet es y=20x-58
Dann ist das ja eigentlich wenn man nicht so dumm ist wie ich und nicht ableitet, leichter als wenn nur nach der Tangente an der Stelle x gefragt wird? Die Schritte sind ja die selben nur hier ohne y zu berechnen
Erst ableiten, dann die Steigung ausrechnen.
f'(x) = 6x + 2
Oh Gott... heute klappt mal wieder gar nichts... aber angenommen ich hätte es nun abgeleitet... keine Ahnung was los ist... 😔 ist ja eigentlich total logisch dass man das erst ableitet...
Zu deinen Fragen 2 und 3 kann ich leider nichts beitragen.
Zu 2. Wenn du (1/f(1)) dann musst du x=1 in die Funktion einsetzen und nach y auflösen dann hast du den Wert also stimmt deine Behauptung.