Spezielle Relativitätstheorie Referat?
Hey:)
ich muss ein Referat zum Thema „Grundlagen der speziellen Relativitätstheorie und Einsteins Postulate“ halten. Leider hab ich keinen Plan vom Thema und weiß nicht was ich machen soll. Könnte mir jemand helfen?
2 Antworten
Die Lichtgeschwindigkeit ist laut Einsteins Relativitätstheorie in jedem Bezugssystem absolut und immer gleich, egal ob wir auf der Erde messen oder in einer Rakete, die sich relativ zur Erde annähernd lichtschnell bewegt. Wird z.B. von der Erde aus ein Lichtstrahl zur Rakete geschickt, messen wir für diesen Lichtstrahl sowohl auf der Erde als auch von der schnellen Rakete aus immer die absoluten 300'000 km/s und nicht, wie man etwa meinen könnte, in der Rakete nur noch eine Differenz zur eigenen Geschwindigkeit.
Die Lichtgeschwindigkeit ist absolut, weil sich die relativen Größen Raum und Zeit entsprechend verändern. Während das eigene Bezugssystem, sei es auf der Erde oder in der Rakete, einem räumlich und zeitlich immer „normal“ erscheint (gewohnte Distanzen, gewohnter Zeitablauf), erscheint das Bezugssystem des anderen relativ zu einem selber bewegten Beobachters verzerrt. Der Raum ist in der Länge geschrumpft und die Zeit gedehnt, sodass sich für das Licht aus Strecke durch Zeit immer dieselbe Geschwindigkeit ergibt.
Für Masse ist die Lichtgeschwindigkeit nur annäherungsweise erreichbar, da die Masse bei Lichtgeschwindigkeit gegen unendlich tendiert und damit die zur weiteren Beschleunigung benötigte Energie ebenfalls.
Auch durch Addition hoher Geschwindigkeiten lässt sich die Lichtgeschwindigkeit nicht erreichen. Wenn sich z.B. eine Rakete relativ zur Erde mit 75% Lichtgeschwindigkeit bewegt und von dieser Rakete eine zweite Rakete startet, wieder mit 75% Lichtgeschwindigkeit relativ zur ersten Rakete, beträgt die Geschwindigkeit relativ zur Erde nicht 150%, sondern durch die veränderten Größen Raum und Zeit nur 96% der Lichtgeschwindigkeit. Die Formel dazu steht im Anhang.
https://de.wikipedia.org/wiki/Relativistisches_Additionstheorem_f%C3%BCr_Geschwindigkeiten
Hallo MrsNeugierig443,
die übliche Beschreibung von Zeit als etwas, das „vergeht“, steht dem Verständnis der Speziellen Relativitätstheorie (SRT) im Weg.
Was wir beobachten können, sind ja Ereignisse und Vorgänge, die bereits in der Vergangenheit liegen. Zum „Raum, wie er jetzt ist“ haben wir keinen Zugang. Erst im Rückblick lässt sich ausrechnen, wann ein Ereignis stattgefunden haben muss.
Die SRT geht hier noch einen Schritt weiter: Was alles „jetzt“ ist, ist für räumlich getrennte Ereignisse nicht einmal verbindlich definiert. Übrigens gilt dasselbe für das „Hier“ bei zeitlich getrennten Ereignissen, und zwar schon in der NEWTONschen Mechanik (NM).
Das Relativitätsprinzip von GALILEIGALILEI war im 17. Jhd. einer der Ersten, die glaubten, dass sich die Erde täglich einmal um die eigene Achse und jährlich einmal um die Sonne dreht. Damit eckte er nicht nur bei der Kirche an, sondern auch bei seinen Kollegen: Wie kann man sich so schnell bewegen und nichts davon merken?
GALILEIs Antwort ist das Relativitätsprinzip (RP) Wenn wir uns relativ zueinander bewegen und jeder sich selbst als den stationären Beobachter ansieht, wirst Du für einige physikalische Größen andere Werte herausbekommen als ich, aber die grundlegenden Beziehungen zwischen diesen Größen (= Naturgesetze) sind gleich.
Was man spüren könnte, sind Änderungen der Geschwindigkeit; bei der Erde treten sie auf, sind aber zu gering, um sich auf kleinem Raum in kurzen Zeiten bemerkbar zu machen.
Das RP relativiert die Gleichortigkeit zweier Ereignisse, etwa den ersten und den letzten Schluck aus einer Tasse Kaffee. Nehmen wir an, ich trinke den Kaffee in 6min aus. Natürlich bleibe ich dabei gemütlich sitzen. Die Erde allerdings transportiert mich mit etwa 1000km⁄h ostwärts. Wenn Du mit einem Flugzeug so schnell in westlicher Richtung fliegst, dass Du die Sonne stundenlang immer an derselben Stelle stehen siehst, könntest Du sagen, dass Du stationär bist, die Erde sich unter Dir weg dreht. So gesehen trinke ich meinen Kaffee 100km weiter östlich aus als ich ihn angetrunken habe.
MAXWELLs Wellengleichung und EINSTEINs PostulatZu den Naturgesetzen gehören auch die Gesetze der Elektrodynamik, die erst im 19. Jhd. entdeckt wurden. Direkt aus ihnen folgt die elektromagnetische Wellengleichung (EMW), der auch das Licht „gehorcht“. Sie ist also auch ein Naturgesetz.
Das Besondere an der EMW ist, dass sie im materiefreien Raum gilt (bei der Ausbreitungsgeschwindigkeit von Schallwellen stellt sich die Frage „relativ zu was“ nicht, da das klar ist: relativ zu dem Körper, in dem sich der Schall ausbreitet).
Wenden wir aber das RP konsequent auf die EMW an, ergibt sich daraus automatisch EINSTEINs Postulat: Jeder Beobachter muss für die Ausbreitungsgeschwindigkeit des Lichts relativ zu sich denselben Betrag c messen.
Ein Gedankenexperiment mit RaumstationenStell Dir vor, Du befindest Dich auf einer Raumstation A irgendwo weit weg von Sternen und Planeten (das ist die ideale Umgebung, um SRT zu betreiben).
In einer gewissen Entfernung von Dir befindet sich eine weitere Raumstation B, die sich relativ zu Dir nicht bewegt. Eine dritte Raumstation C mit mir an Bord kommt aus dieser Richtung (mit leichtem Versatz) auf Dich zu, mit dem Tempo v = c·β.
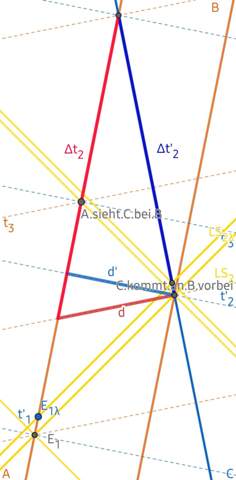
Du schickst zur Zeit t₁ ein Lichtsignal richtung B und bekommst das Echo zur Zeit t₃ zurück. Unter der Annahme, dass Deine Station ruht, muss die Entfernung
(1.1) d = ½·c·(t₃ − t₁)
sein. Für den Zeitpunkt der Reflexion kommst Du auf das arithmetische Mittel
(1.2) t₂ = ½·(t₃ + t₁).
Zu dieser Zeit komme ich gerade mit C an B vorbei und bekomme das Signal ebenfalls - zusammen mit dem Echo eines Signals, das ich zu einer Zeit t₀ abgeschickt habe, und wir werden uns zur Zeit t = t₂ + d⁄v an Dir vorbeikommen. Dies sind die Zeiten nach Deiner Uhr, der Borduhr von A. Die Zeiten nach meiner Uhr, der Borduhr von C, nenne ich t'₀, t'₁, t'₂ und t'₃.
Wenn wir nun den Zeitnullpunkt t = t' = 0 auf unsere Begegnung festlegen, ist also
(2.1) t₂ = −d⁄v = d⁄(c·β)
(2.2) t₁ = −(d⁄v + d⁄c) = −(d⁄v)∙(1 + β) = t₂·(1 + β)
(2.3) t₃ = −(d⁄v − d⁄c) = −(d⁄v)∙(1 − β) = t₂·(1 − β).
Das RP verlangt Symmetrie zwischen uns, d.h., t'₂ muss wie t₂ zwischen t₁ und t₃ liegen, aber nicht im Sinne des arithmetischen, sondern des geometrischen Mittels zwischen den Beträgen bzw. der Dauer bis zur Begegnung, d.h.
(3.1) |t'₂|⁄|t₃| = |t₁|⁄|t'₂| = √{(1 + β)/(1 − β)} =: K,
was übrigens auch der Faktor ist, um den Frequenzen größer ankommen als sie abgesendet werden. Anders ausgedrückt ist
(3.2) |t'₂| = √{|t₁|·|t₃|} = |t₂|√{(1 + β)(1 − β)} = |t₂|√{1 − β²}.
Dieses Ergebnis wird oft irreführend „Zeitdilatation“ genannt. Zugleich folgt daraus, dass man unter der Annahme, dass ich ruhe, für den Abstand zwischen A und B nur
(4) d' = d∙√{1 − β²}
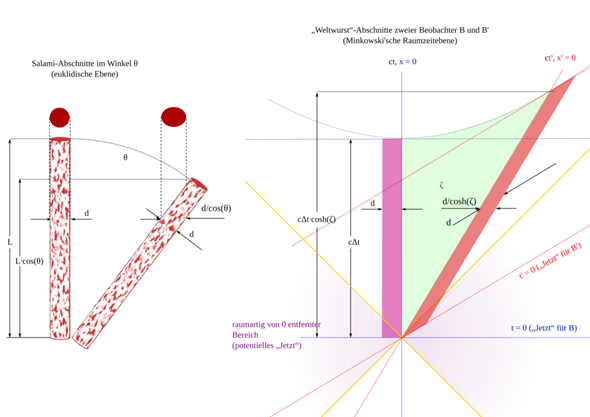
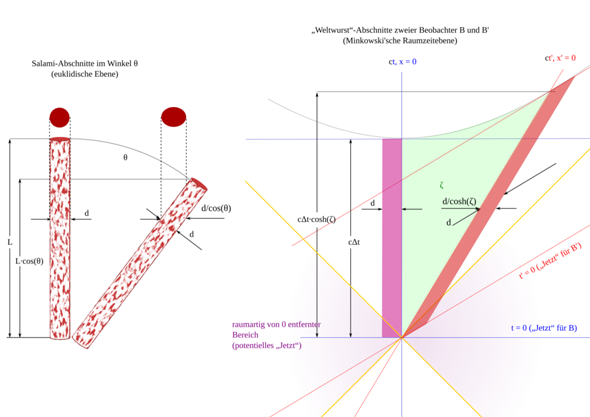
herausbekommt, was irreführenderweise „Längenkontraktion" genannt wird. Schließlich handelt es sich nicht um eine und dieselbe Strecke, die mal kürzer und mal länger wäre, sondern um zwei verschiedene raumzeitliche Verbindungslinien, die einfach unterschiedlich lang sind.
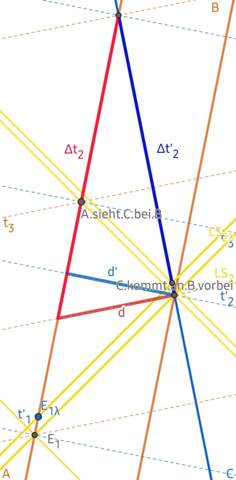
Ich nenne die „Längenkontraktion“ gern einen Schrägschnitt durch die Weltwurst, in Anlehnung an eine Salami, die man schräg anschneidet.