Warum ist sin²(x) + cos²(x) = 1?

Das ist der sogenannte trigonometrische Pythagoras. 

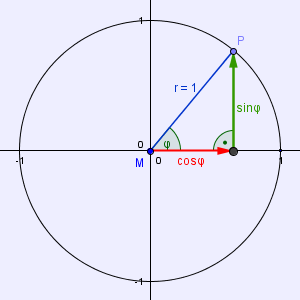
Wenn Du Dir den Einheitskreis ansiehst und ein rechtwinkliges Dreieck einzeichnest, wird schnell klar, warum der Satz gilt. sin(x) und cos(x) sind die beiden Katheten (der Nenner ist 1, fällt also weg), 1 ist die Hypotenuse.

Daraus folgt dann sin²(x) + cos²(x) = 1² - der trigonometrische Pythagoras.

Hallo,

Pythagoras läßt grüßen.

In jedem rechtwinkligen Dreieck gilt:

sin (Phi)=Gegenkathete/Hypotenuse

cos (Phi)=Ankathete/Hypotenuse

Gegenkathete=G, Ankathete=A, Hypotenuse=H

sin²(Phi)=G²/H²

cos²(Phi)=A²/H²

sin²(Phi)+cos²(Phi)=G²/H²+A²/H²=(G²+A²)/H²

Da die Summe der Quadrate über den Katheten in jedem rechtwinkligen Dreieck gleich dem Quadrat über der Hypotenuse ist, 
gilt: sin²(Phi)+cos²(Phi)=(G²+A²)/H²=H²/H²=1

Herzliche Grüße,

Willy

Das hebt sich gegenseitig auf. Die sind ja um 180 Grad verschoben.

Mario