Satz des Pythagoras. Wie löse ich diese Aufgabe?
-Eine Mauer ist genau so lang wie eine Leiter, welche im Abstand von 120cm zu der Mauer steht. Sie lehnt 20cm unter dem Mauernende an. Wie groß ist die Leiter.
Schreibe morgen einen Test, und bekomme einfach diese Aufgabe nicht hin.
4 Antworten
Hallo,
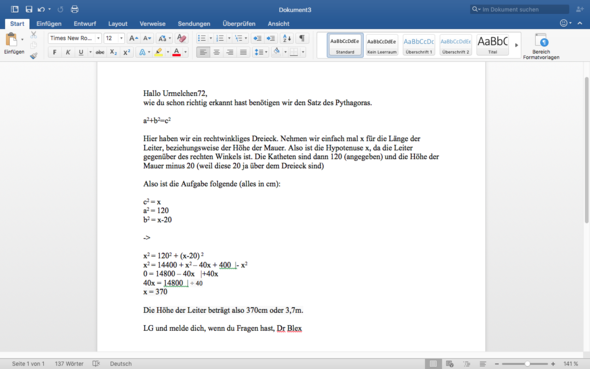
weil ich leider nicht weiß, wie man "hoch2" hier einstellen kann, habe ich dir die Antwort auf Word geschrieben, da es so übersichtlicher ist.
Achso. Deshalb auch das Mac :'D
Und dankeschön, das werde ich hoffentlich nicht brauchen ^^
Ich muss natürlich verbessern, dass ich bei c^2=, b^2= und a^2= bei den Werten jeweils das ^2 vergessen habe!
Außerdem gern geschehen. Ich wünsche dir viel Glück!
A^2+B^2 = C^2
A^2 = gesucht
B^2 =Abstand zwischen Mauer und Leiter (also die 20cm )
C^2= 120cm
Also muss man rechnen
Größe Leiter^2+ 20cm^2 = 120 cm^2 , das dann umstellen also -20cm^2 machen. Also steht da:
Größe Leiter^2= 120cm^2 - 20cm^2 ja und das halt auflösen.
Also so würde ich es machen ich weiß nicht ob es stimmt. Und kann auch keine Garantie geben. Ich hoffte es hilft dir
Lg Cookinggirl
Grobe Durchsicht, aber ich glaube das stimmt nicht. Das Umstellen hast du ja fertig. Deine Leiter ist dann so ca wurzel aus 1040 cm lang. Das ist ja nichtmal eine kleine Haushaltsleiter.
B^2= die freie Fläche. Also von dem höchsten Punkt der Mauer 20cm nach unten gehen, und da liegt die Leiterspitze an. Ist schwer in Worte zu fassen
x^2=120^2*(x^2-20), denke ich mal :)
hilft mir auch nicht viel weiter. Zumal es ja in diesem Fall x^2+y^2=x^2 heißt und nicht x^2-20 oder?
Und wenn der Endpunkt der Leiter 1,20m unterhalb der Mauerkrone enden würde? Achte auf die Klammer!
A^2 + B^2 = C^2 das ist die Formel
Die Katheten sind die kurzen Seiten und die längste ist die Hypertenose ist am einfachsten zu rechnen mach am besten eine Skizze
Achja für ein ² einfach Strg und Alt tasten gedrückt halten und dann die entsprechende Zahl