Mathe Satz des Pythagoras (Aufgabe:Länge x berechnen)?

Hallo,
wie kann man diese Aufgabe mit dem Satz des Pythagoras lösen.
a² + b² = c²
5 Antworten
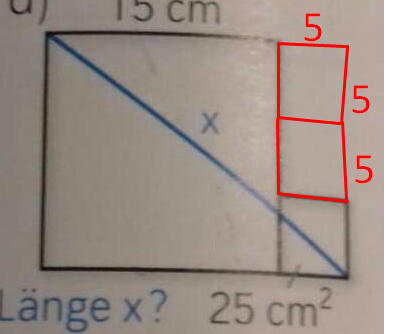
Du hast 2 Vierecke. Jede Seite ist gleich lang.
Großes Viereck: 15cm jede Seite.
Kleines Viereck: 5cm jede Seite. Dort steht "25cm²", weil cm² Länge mal Länge ist, also eine Fläche. 5*5 ist 25.
Eine einfache Möglichkeit sowas zu lösen wäre wie folgend:
Du erweiterst dein großes (15cm) Viereck einfach nach rechts. Siehe Bild. In 15cm passt 5cm DREI mal rein, das heißt du kannst noch zwei 5cm Würfel hinzufügen.
Nun hast du ein aus den beiden Vierecken ein RECHTECK gebildet. Das Rechteck ist 20cm lang (oben und unten), und 15cm hoch(rechts und links).
Der Satz des Pythagoras kommt hier ins Spiel: Du willst die diagonale linie X berechnen. Du hast die Länge 20cm und 15cm gegeben. 20cm kannst du dein a nennen, 15 dein b. Ist aber eigentlich egal in diesem Fall.
Formel: 20² + 15² = 625.
Aus 625 musst du noch die Wurzel ziehen, denn es ist ja c² und nicht c. Du willst c.
Die Wurzel von 625 ist 25.
Deine Antwort lautet also: X hat eine Länge von 25cm.

- Seite vom kleinem Quadrat zurechnen --> Wurzel von 25= 5
- 15cm (Seite von oben) + 5cm (Seite vom kleinen Quadrat) = 20cm Das heisst nun: Seite unten= 20cm und Seite links 15cm
- 20 hoch2 + 15 hoch2 = 625
- Wurzel von 625= 25
- x=25
Dieses Thema ist schon eine Weile her, darum kann ich nicht zu 100% sagen das es stimmt. Viel Glück noch ;)
Glaub die Aufgabe ist nur lösbar wenn man annimmt das beide Rechtecke Quadrate sind, das Grosse 15cm x 15cm und das Kleine 5 cm x 5cm. Allerdings sieht gerade das kleine Rechteck nicht wirklich quadratisch aus.
Dann wäre es:
x² = 15²cm² + 5²cm²
x² = 250cm²
x = 15,811cm
Berechne die Länge des kleinen Quadrates und addieren dazu + 15.
Jetzt kannst du x berechnen.
Mit der Formel, die du da hast