Polynomfunktion dritten Grades zeichnen?
Gegeben sind folgende Eigenschaften einer Polynomfunktion dritten Grades:
- f(0)=1
- f'(0)=0
- An der Stelle x=2 berührt f die x-Achse
- f'(x)>0 für x ∈ (-∞;0)
Wer mir diesen Graphen zeigen könnte und die Ableitung der ist einfach spitze. Bitte helft mir!
Danke im Voraus!!
2 Antworten
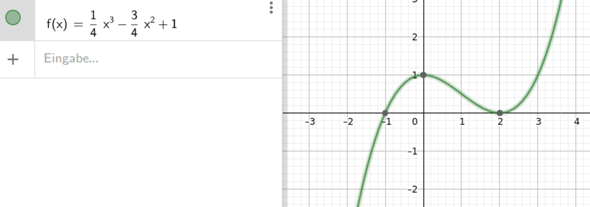
du hast einen Punkt (0/1) , der zugleich ein Extremum ist.
bei x = 2 eine Berührstelle. Berührstellen sind auch immer Extrema.
die Steigung zwischen (-∞;0) ist positiv
wegen letzterem muss die Kurve von links unten kommen , geht durch (0/1) , dort ist ein Maximum, denn sie muss bei x = 2 die x-Achse berühren , dort muss dann ein Minimum sein .
Sie geht für x gegen +∞ dann weiter gegen +∞.
Die Ableitung einer Fkt dritten Grades ist eine Parabel.
Man weiß schon , dass sie bis x = 0 im positiven Bereich sein muss.
Weil bei x = 0 ein Extr ist , geht die P dort durch und unter die x-achse und bei x = 2 wieder durch und danach über die x-Achse . Parabel mit Nullstellen bei 0 und +2 und der Scheitel ist genau dazwischen bei x = 1 . Dadurch Zusatzinfo : bei f(x) ist ein Wendepunkt bei x = 1
der y-Achsenabschnitt ist (0|1), dort hat das Schaubild eine waagrechte Tangente
bei (2|0) hat man einen Extrempunkt
wegen f'(x)>0 für x<0 ist das Schaubild bis zum y-Achsenabschnitt steigend.
Das Schaubild kommt von -oo und geht nach +oo. Bei (0|1) hat das Schaubild einen Hochpunkt, bei (2|0) einen Tiefpunkt
Polynomfunktion 3. Grades: f(x)=ax³+bx²+cx+d
Ableitung: f'(x)=3ax²+2bx+c
f(0)=1 ==> d=1
f'(0)=0 ==> c=0
Berührpunkt mit der x-Achse bei x=2, also Nullstelle mit waagrechter Tangente:
f'(2)=0 ==> 12a+4b=0
f(2)=0 ==> 8a+4b+1=0
------------------------------------
a=1/4
b=-3/4
@MichaelH77 : dürfte ich so lästig sein und Dich bitten mir auch gleich die zweite Frage zu diesem Thema zu beantworten? https://www.gutefrage.net/frage/mathematik-polynomfunktion