Mathematik: Ableitung einer Funktion 4. Grades
Hallo!
Ich habe die Ableitung einer Funktion gegeben. Der Graph berührt die x-Achse bei x = -2 und schneidet die x-Achse bei x = 0 und x = 3. Daraus folgt also, dass die Ursprungsfunktion vierten Grades sein muss. Was sagt mir aber die doppelte Nullstelle der Ableitung über die Ursprungsfunktion aus?
Ich bedanke mich für die Antworten! :-)
3 Antworten
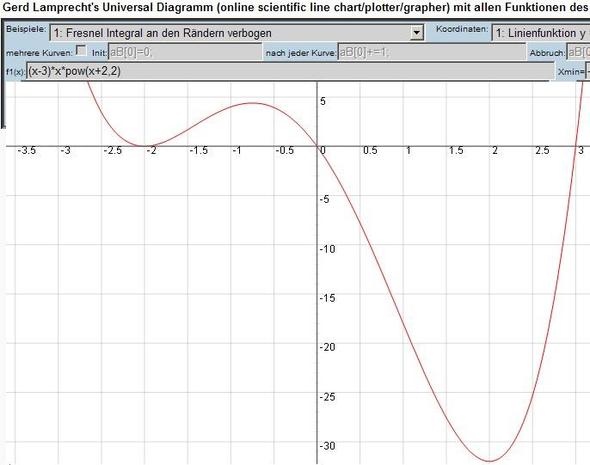
Wenn der Graph die x-Achse bei -2 nur berührt (und nicht schneident), kann das durch (x+2)² ausgedrückt werden. Damit ergibt sich:
per http://www.gerdlamprecht.de/Liniendiagramm_Scientific_plotter.htm
(x-3)* x* pow(x+2,2) siehe Bild
eine Gleichung 4. Grades. mit pow(x,y) = x hoch y
Aber Achtung: wenn das die Ableitung ist (oben steht ja "Ableitung ... gegeben") dann ist die Ursprungsfunktion das Integral davon, also eine Funktion 5. Grades (Aufgabe ist leider nicht eindeutig, ob Graph von Ableitung oder von Ursprungsfunktion beschrieben ist)
Es gibt auch keine Maxima oder Hinweise, ob die Funktion nach oben oder unten offen ist: Negation ginge auch: -(x-3)* x* pow(x+2,2)
Also mit vierten Grades bist du auf dem Holzweg. Das ist eine Funktion 3. Grades. Denn Abgeleitet ergibt sie eine Funktion 2. Grade. Und die dir vorliegenden Funktion (Ableitung f'(x)) ist eine Parabel und damit eine Funktion 2.Grade.
Die Funktion sieht ungefähr so aus... D.h. die Funktion ist 4. Grades! Oder täusch ich mich da?
