Ordnen Sie die Graphen zu und begründen Sie ihre Zuordnung?
Leute kann mir jemand bei der Aufgabe helfen? Leider habe ich keinen blassen schimmer...
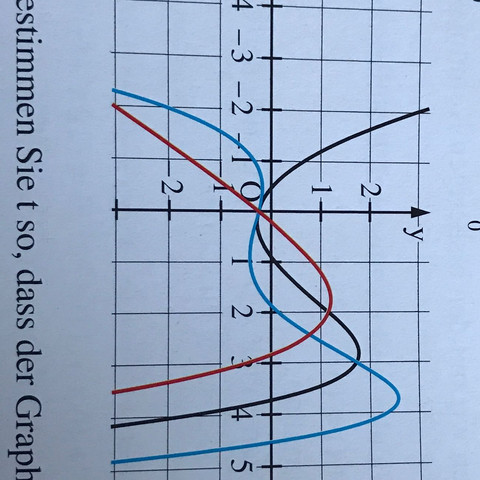
Fig.1 zeigt die Graphen einer Funktion f, ihre Ableitung f‘ und einer Stammfunktion F.
Ordnen Sie die Graphen zu und begründen Sie ihre Zuordnung.
Vielen Dank im Vorraus!
3 Antworten
Die Ableitung von f (f') gibt die Steigung von f an der gleichen Stelle an.
Die Funktion f ist hingegen die Ableitung der Stammfunktion F.
Es gibt also einen Graphen, der die Steigung des anderen angibt. Und es gibt einen Graphen, der die Steigung der Steigung angibt.
Jetzt musst du nur noch an ein paar Stellen überprüfen, was auf welche Linie zutrifft.
Wenn die Funktion eine Steigung von Null hat, hat ihre Ableitung einen Funktionswert von 0 an dieser Stelle.
Das reicht zum lösen dieser Aufgabe schon aus.
Blau ist die Stammfunktion F, schwarz die Funktion f und rot die Ableitung f'. Es handelt sich um ganzrationale Funktionen 4., 3. und zweiten Grades, das erkennt man an der Anzahl der Extremalpunkte. Eine ganzrationale Funktion nten Grades hat maximal n-1 Extremalpunkte.
Dann lies bitte meinen letzten Satz. Eine Funktion 2ten Grades ist z.B. eine Parabel, sie hat genau einen Extremalwert.
Wieso 4.,3. und2. Grades? Ich sehe nur 3.,2. und 1 extrempunkt...