O Notation quadratisch linear?
Wieso ist n² nicht in O(n), obwohl doch z.b. für c=100 (also 100*n) >1² ist.
6 Antworten
Was ist denn dann deine Schranke? (Spoiler: Die kann es nicht geben). Schau dir nochmal die Definition der O-Notation an:
Um zu zeigen, dass eine Funktion g in O(f) liegt, musst du ein positives c und ein natürliches n0 finden, sodass die obige Ungleichung erfüllt ist. Wählst du nun c = 100, müsstest du noch ein n0 finden, sodass für alle n > n0
gilt. Dass das nicht funktionieren kann, zeigt man schnell durch elementare Abschätzungen. Umgekehrt wird ein Schuh draus.
LG
Wie habt ihr das definiert? n^2 ∈ O(n), wenn gilt:
Dies ist offensichtlich falsch.
Wie habt ihr denn die O-Notation definiert. Wenn ich beispielsweise bei der recht üblichen Definition bleibe, wie sie auf Wikipedia zu finden ist...
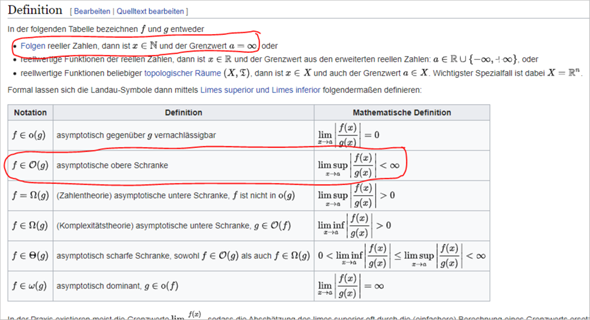
https://de.wikipedia.org/wiki/Landau-Symbole#Definition
Dann müsste für n² in O(n) gelten...

Das ist aber falsch. Stattdessen ist...

============
Ansonsten mit...

Dann behauptest du, dass C = 100 ein passendes C wäre, wenn ich dich richtig verstanden habe.
Jedoch muss ja das gleiche C für fast alle n passen. Und für n ≥ 100 passt dieses C nicht mehr. Denn für C = 100 und n ≥ 100 ist eben nicht n² < 100 n, sondern n² ≥ 100 n.




Eine Funktion f ist in O(g), wenn es ein N und ein a>0 gibt, sodass für alle n>N gilt:
f(n) < ag(n)
Das stimmt zwar, dass 100n > n² für n = 1 ist, aber für größere n ist das nicht mehr der Fall, nimm zb 1000, dann hat man: 100 * 1000 = 100000 < 1.000.000 = 1000 * 1000
(Diese Definition ist äquivalent zu der von @bert00712)
Ne das ist nicht richtig. Also 4^n ist immer kleiner als 6^n, somit ist 4^n in O(6^n), aber mit welcher Konstante willst du 3^n multiplizieren um auf 6^n zu kommen? Wenn man das Grenzwert-Kriterium von bert00712 anwendet dann bekommt man 4^n / 3^n, das ist ungefähr 1.333... ^n und dieser Wert geht für n gegen unendlich auch gegen unendlich
Nein. Dafür müsstest du ja eine Kostante finden, so dass c * 3^n > 4^n ist.
Und das ist ja nicht so, 4^n/3^n ist (4/3)^n und das wird mit wachsendem n beliebig groß.
Auch 3^n und 6^n unterscheiden sich nicht durch eine Konstante.
Es muss ein n0 < n existieren, sodass für alle n gilt n^2 <= c*n
Da reicht es nicht einen Wert einzusetzen
Also ist z.B. 4**n in O(3**n), da z.B. 4**n immer kleiner als 6**n ist?