Mathematisches Problem (Kreise im Dreieck)
In ein gleichschenkliches Dreieck mit der Basis c = 8 cm und den Seiten a = b = 12 cm werden fortwährend Kreise mit möglichst großen Radien so einbeschrieben, dass der nächstkleinere Kreis die Seiten a und b mit den vorhergehenden Kreis berührt.
Meine Frage wären:
a. Bestimme die Summe der Umfänge aller Kreise. b. Welchen Flächeninhalt haben alle Kreise zusammen? c. Wie groß ist der prozentuale Anteil der Kreisfläche an der Dreiecksfläche?
Dies ist die mündliche Hauptschulprüfung der kleinen Schwester eines Bekannten und ich als Abiturient habe damit meine Schwierigkeiten. Könnte mir jemand helfen? Anbei auch ein Foto der Aufgabe. (Die kleinen Punkte über den Kreisen sind sinnbilder für unendlich weiterer Kreise.)
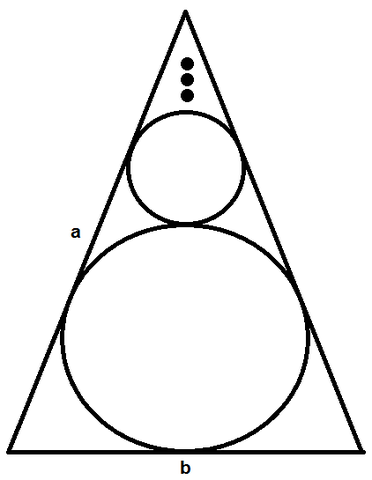
5 Antworten
Das ist eine Abfolge der Bestimmung der Innenkreise über die Winkelhalbierenden (konstruktiv), die man aber auch rechnerisch bestimmen kann. Da Alpha und Beta bekannt sind kann das Dreieck zum Inkreismittelpunkt des großen Kreises berechnet werden und deren Höhe ist der Radius! Nun Zieht man von der Höhe des ganzen Dreiecks den Durchmesser des großen Inkreises ab und hat dann den oberen Dreiecks"Stumpf" und ein kleineres Dreieck, für das man auf die gleiche Weise den nächsten Inkreis bestimmt.
... ist mir leider ein grober Fehler unterlaufen, weil ich die Winkelhalbierenden im Dreieck mit den Höhen verwechselt habe. Die invaliden "grauen Zellen" lassen grüßen !
sorry
Die gemeinsamen (waagrechten) Tangenten der Kreise teilen das Dreieck in
(unendlich) viele Trapeze. Deren Mittelparallele ist näherungsweise gleich dem
Durchmesser D des betr. Kreises. Auch die Höhe ist D, die Fläche also ca. D².
Die Kreisfläche ist ¼πD², das Verhältnis Kreisfläche zu Trapezfläche ist daher
¼π ≅ 0,795 = 79,5%. Das ist auch das Verhältnis der Summe
aller Kreisflächen zur Dreiecksfläche (in Wirklichkeit etwas weniger).
Die Summe aller Durchmesser ist die Höhe h des Dreiecks.
Nach Pythagoras ist h² = 128.
Der Umfang ist immer das π-fache des Durchmessers,
daher ist die Summe aller Umfänge π • h.
Über den Rest muss ich noch nachdenken.
Das hat ja Universitäts-Niveau!
In welchem Bundesland ist diese Aufgabe Thema einer mündlichen Hauptschulprüfung?
Die ist wirklich keine weiche Nuss. Nicht weil man hier sonderlich schwierige Rechnungen anstellen muss, sondern weil man um einige Ecken denken muss, um die Lösungen zu sehen.
Eine solche Aufgabe würde ich eher in einer Matheolympiade vermuten oder, wie Stekum andeutet, in einem Eignungstest für eine Studienzulassung.
Exakte Lösung von b) und c) . . .
Der Durchmesser des Inkreises (größten, untersten Kreises) ist ½h = 4√2.
Daher ist die Mittelparallele des unteren Trapezes 6 und sein Flächeninhalt ist
24√2 (¾ der ganzen Dreiecksfläche). Die Fläche des Kreises ist 8π
und das Flächenverhältnis 8π / 24√2 = ⅙π√2 ≅ 74%.
Die ganze Figur setzt sich aus einer unendlichen Folge selbstähnlicher Trapeze mit jeweils einem eingebetteten Inkreis zusammen.
Um den Flächenanteil aller Kreise zum gesamten Dreieck auszurechnen (Aufgabe c) genügt es, das unterste Trapez zu betrachten.
Daraus kann man dann auch den absoluten Anteil (Aufgabe b) ausrechnen, indem man das Flächenverhältnis des ganzen Dreieckes und des untersten Trapezes bestimmt.
Trotzdem eine knifflige Aufgabe - ich bin mir sicher, da gibt es noch eine "elegantere" Lösung für b und c.
Ich bleib dabei: Für eine Hauptschulprüfung ganz schön heftig.
Zu meinen Zeiten galt die Regel: In die mündliche Matheprüfung gehst Du entweder, um die Chance zu bekommen, die kippelnde 2+ der schriftlichen zu einer 1- zu verbessern, oder um aus der satten 5 eine gnädige 4- machen.
In beiden Fällen ist diese Aufgabe ungeeignet. Für letzteres viel zu schwer für ersteres ist die Zeit zu knapp. ;-)
Hallo, UlrichNagel
In Anlehnung an Deine Antwort erhalte ich bei meiner Herleitung für die Durchmesser der Innenkreise
d(n) = (3/4)^n * h/4 ( n = 1; 2; 3; ... ∞ )
Die Summe der Durchmesser d(1) bis d(n) ist die Höhe (h) des Dreiecks.
LG