Mathematik Integralrechnung Hilfe?
Hallo :) bin gerade am verzweifeln bei Mathematik wiedermal 😣😅 Die Aufgabe:
Inhalt der Fläche berechnen, die von den Graphen der Funktion f und g und den gegebenen Geraden begrenzt wird.
1) f(x)=x^2+4 g(x)=x+3 x=-1 x=1
2) f(x)=x^2+4 g(x)=2x+4 x=-1 x=1
3) f(x)=Wurzel von x g(x)=1 x=0 x=4
4) f(x)=sin(x) g(x)=cos(x) x=π/2 x=π
Hab jetzt mehrmals welche durchgerechnet und trotzdem das Gefühl dass ichs falsch gemacht habe. Also ich verstehe, wie man die Fläche berechnet aber ich scheine irgendetwas falsch zu machen.
1)x^2-x+7 (Funktion nach Differenz)
1/3x^3-1/2x^2+7x (Stammfunktion)
Nach einsetzten der x-Werte:
44/3
1) Korrektur: x^2-x+1
F(x)=1/3x^3-1/2x^2+x
Endergebnis 8/3
2 Antworten
3)
Mach dir einen Graph oder eine Skizze !
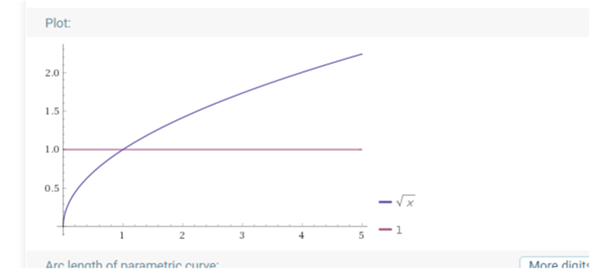
so sieht f(x) = wur(x) und g(x) =1 aus
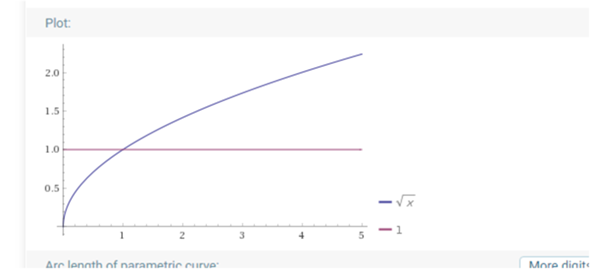
du brauchst den Schnittpunkt SP
und dann zwei Differenzen von Integralen
Int ( 0 bis SP ) von ( g(x) - f(x) )
plus
Int ( SP bis 4 ) von ( f(x) - g(x) )
Also mal g - f und dann f - g !!!!
..................................
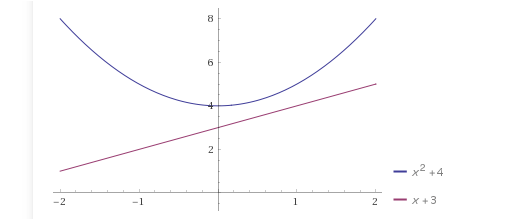
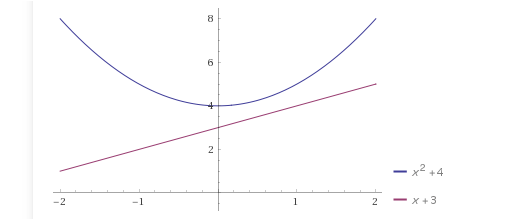
Bei 1 ) ist das nicht so problematisch : da reicht
int ( -1 bis +1 ) von (x² + 4 ) - ( x + 3 ) = (x²-x+1)........int ist 1/3 x³ - 1/2 x² + x + C
Hallo Katja,
zeig doch am besten ein Foto deiner Lösung, dann kann man schnell sehen, ob du alles richtig gerechnet hast oder nicht!
Habs ergänzt ich weiß nicht ob meine Schrift so leserlich ist ^^