Sind meine Überlegung zu diesen Aufgaben richtig?

Kurze Frage zu der Aufgabe c bei der ersten Aufgabe muss ich gucken ob die beiden Geraden senkrecht zueinander verlaufen hab ich gemacht und das tun sie dann den Schnittpunkt da man ja in der mittleren Zeile der beiden geraden die unbekannten streichen kann haben diese auch einen Schnittpunkt und da hab ich jetzt 0|-3|-6 raus ist das richtig? Und bei der zweiten Aufgabe ist das dann genau der gleiche Fall schreib ich das dann einfach da hin oder muss ich irgendwas noch ausrechnen? Oder kann es sein dass ich da etwas komplett falsch gemacht habe?
4 Antworten
der Schnittpunkt ist (3|-3|3). Dieser Punkt ist der Stuetzpunkt von beiden Geraden. für r=0 und s=0 erhält man diesen Schnittpunkt
die Rechtwinkligkeit wird mit dem Skalarprodukt der beiden Richtungsvektoren nachgewiesen, das muss null sein, was hier der Fall ist
die Ebene enthält den gemeinsamen Punkt und die beiden Richtungsvektoren der beiden Geraden.
man braucht da nichts rechnen, man sieht sofort, dass der Punkt auf beiden Geraden liegt
Den Schnittpunkt kannst du direkt ablesen. Beide Geraden haben nämlich denselben Stützvektor, also ist der Schnittpunkt S (3|-3|3).
Bei der Ebenenaufgabe stellst du eine Ebenengleichung auf. Dabei ist der Schnittpunkt der Stützvektor der Ebene und die beiden Richungsvektoren der beiden Geraden jeweils die beiden Spannvektoren der Ebene. Dann mithilfe des Taschenrechners oder LGS gucken, ob halt der vorgegebene Punkt P in der Ebene liegt. Oder Du formst die Ebenengleichung in die Koordinatenform um, falls ihr das hattet und setzt für x,y,z die Werte von Punkt P ein und schaust, ob eine wahre Aussage rauskommt. Falls ja, liegt der Punkt in der Ebene, falls die Aussage falsch ist, dann liegt der Punkt nicht in der Ebene.
https://imgur.com/a/erfQzoX hab das jetzt so gemacht wie muss ich dass denn jetzt weitermachen?
Die beiden Geraden haben ja den gleichen Stützpunkt (Stützvektor) a(3/-3/3)
2 Vektoren stehen senkrecht aufeinander,wenn das
Skalarprodukt a*b=ax*bx+ay*by+az*bz=0 ist
also m1*m2=3*1+0*0-1*3=0 Geraden stehen senkrecht aufeinander
Vektorielle Parametergleichung der Ebene E: x=a+r*u+s*v
x=(3/-3/3)+r*(3/0/-1)+s*(1/0/3)
m1=u(3/0/-1) Richtungsvektor von Punkt A(3/-3/3) aus
m2=v(1/0/3) Richtungsvektor von Punkt A(3/-3/3) aus
mit P(7/-3/5) göeichgesetzt
(7/-3/5)=(3/-3/3)+r*(3/0/-1)+s*(1/0/3)
x-Richtung: 1) 3*r+1*s=7-3=4
y-Richtung:2) 0*r+0*s=-3-3=-6
z-Richtung:3) -1*r+3*s=5-3=2
2) ist ein Widerspruch (Unsinn) und damit liegt der Punkt P(7/-3/5) nicht auf der Ebene.
Aber wie kommst du denn bei der Ebene auf 4,-6,2? Das additionsverfahren kann ich ja durch die fehlende zweite Spalte nicht mehr anwenden und ich weiß doch nicht was r und s jetzt sind? Werden die dadurch das die in der mittleren Spalte nicht mehr existieren automatisch gleich null???
Tut mir leid hab nochmal nachgerechnet und dein Ergebnis könnte falsch sein denn ich komme auf das richtige Ergebnis https://imgur.com/a/0NQLuVo hoffe man kann es lesen
bei einem online Rechner kommt auch das selbe raus
Eine Ebene ist durch 3 Punkte eindeutig definiert
Dreipunktgleichung der Ebene E: x=a+r*(b-a)+s*(c-a)
gegeben: 3 Punkte A,B und C
A(ax/ay/az) → Ortsvektor a(ax/ay/az)
B(bx/by/bz) → Ortsvektor b(bx/by/bz)
C(cx/cy/cz) → Ortsvektor c(cx/cy/cz)
Ebenengleichung E: x=(ax/ay/az)+r*[(bx/by/bz)-(ax/ay/az)]+s*[(cx/cy/cz)-(ax/ay/az)]
Richtungsvektor m von Punkt A nach Punkt B → b=a+m → AB=m=b-a
Richtungsvektor m vom Punkt A nach Punkt C → c=a+m → AC=m=c-a
Vektorielle Parametergleichung der Ebene E: x=a+r*u+s*v
also x=(ax/ay/az)+r*(b-a)+s*(c-a)
r und s sind die Parameter der Ebene,nur Zahlen
Das Ganze ist eine Vektoraddition x=a+r*u+s*v
Addition von 2 Vektoren c=a+b
nun führen wir 2 Parameter (Zahlen) r und s ein
ergibt c=r*a+s*b nennt man eine "Linearkombination"
die Parameter r und s (sind nur Zahlen) können frei gewählt werden und somit kann man aus den beiden Vektoren a(ax/ay/az) undb(bx/by/bz) unendlich viel Vektoren c(cx/cy/cz) produzieren
aus die Ebene angewendet
(x/y/z)=(ax/ay/az)+r*(ux/uy/uz)+s*(vx/vy/vz) mit Parameter r und s frei wählbar
ergibt unendlich viele Punkte der Ebene
Ortsvektor ist ein Vektor,der seinen Anfang im Ursprung des x-y-z-Koordinatensystems hat
Großbuchstaben verwendet man für Punkte im Koordinatensystem
Kleinbuchstaben (mit kleinen Pfeil darüber) verwendet man für Vektoren
Beispiel:zeichne ein x-y-Koordinatensystem
gegeben die Punkte A(2/3) und B(5/1)
A(2/3) → Ortsvektor a(2/3)
B(5/1) → Ortsvektor b(5/1)
Richtungsvektor m von Punkt A nach Punkt B → b=a+m → AB=m=b-a
AB=m=(5/1)-(2/3)=(3/-2)
Vektoraddition b=a+m=(2/3)+(3/-2)=(5/1) Ende bei Punkt B(5/1)
Dann versteh ich nicht warum der Rechner online das falsch gemacht hat kann man das auch mit dem Taschenrechner rechnen?
Ich schreib morgen meinen Lehrer mal an ich schreib dann rein was er sagt
zu Punkt 2)
Was hast du den jetzt für die Ebenengleichung heraus ?
Liegt der Punkt P(7/-3/5) auf der Ebene ?
bei 2) steht:Die Ebene enthält die beiden Geraden g: und h:
also liegen beide Geraden in der Ebene E:
E: x=(3/-3/3)+r*(3/0/-1)+s*(1/0/3)
mach nun Proberechnungen mit den Geraden g: und h:
g: x=(3/-3/3)+r*(3/0/-1) mit r=1 ergibt den Punkt P1(x1/y1/z1)
h: x=(3/-3/3)+s*(1/0/3) mit s=1 ergibt den Punkt P2(x2/y2/z2)
P1 und P2 müssen dann auf der Ebene liegen,wenn die Geraden g: und h: beide in der Ebene liegen.
Sorry dass ich nicht geantwortet habe aber 7/-3/5 liegt auf der Ebene E steht selbst in den Lösungen der standardsicherung von nrw drin
Macht nix !
Eine Prüfung auf Rechenfehler-und Tippfehler und auch auf Richtigkeit,müüsen die Fragesteller selber machen,weil ich hier für meine Arbeit keinerlei Geld bekomme.
Hier Beispiel Punkte,Ortsvektoren und Richtungsvektoren im Koordinatensystem.

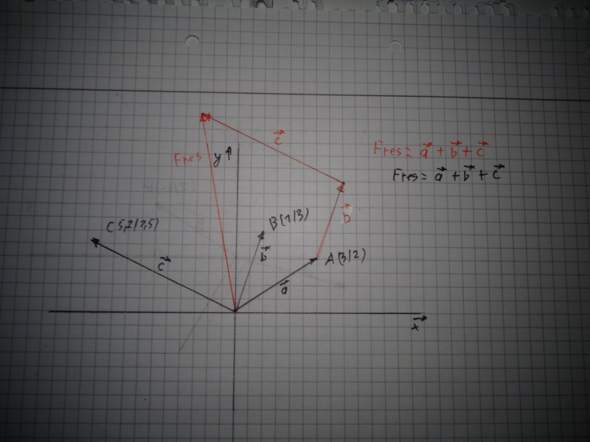
Also rechnerisch dadurch dass r und a in der mittleren Gleichung 0 sind und nur noch die ortsvektoren vorhanden sind werden diese dann gleich 0?