Mathe Steckbriefaufgabe mit Nullstelle?
Meine Aufgabe lautet:
Eine achsensymmetrische ganzrationale Funktion 4. Grades habe eine Nullstelle bei x0=2, sowie einen Hochpunkt bei H(1|9). Bestimmen Sie den zugehörigen Funktionsterm.
Meine Frage ist, ob ich bei der Nullstelle einen abgeleitete Funktion bilden muss, oder eine normale und falls ja: welche Ableitung?
Danke im Voraus
3 Antworten
Eine achsensymmetrische...:
Dann dürfen nur gerade Potenzen drin vorkommen. Daher Ansatz:
f(x) = ax^4 + bx^2 + c
f'(x) = 4ax^3 + 2bx
f'(1) = 4a + 2b = 0
b = -2a
f(1) = 9
ax^4 + (-2a)x^2 + c = 9
a -2a + c = 9
-a + c = 9
c = 9 + a
f(2) = 0
ax^4 + bx^2 + c = 0
a * 16 -2a*4 + c = 0
8a + c = 0
8a + (9 + a) = 0
9a = -9
a = -1
c= 9 -1 = 8
b = -2a = 2
f(x) = -x^4 - 2 x^2 + 8
Probe:
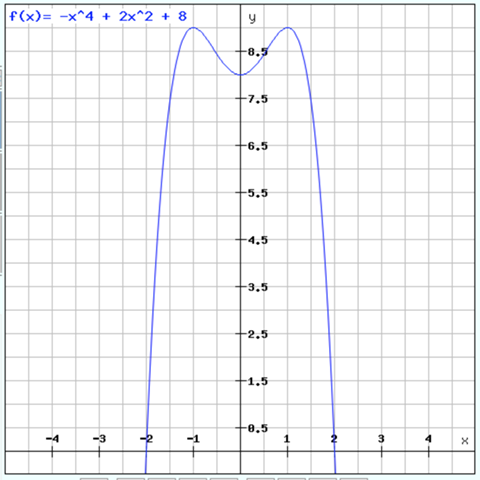
..passt
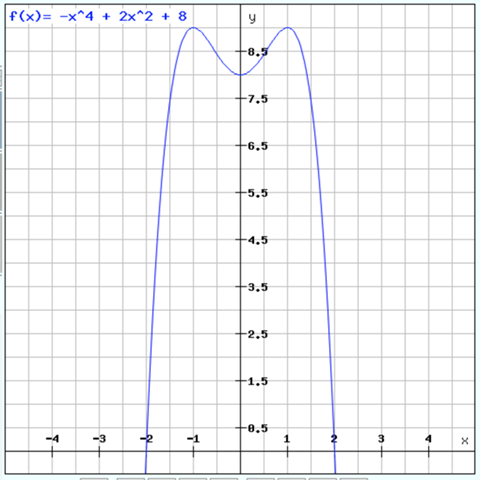
Eine achsensymmetrische ganzrationale Funktion 4. Grades
Das heißt f(x) = ax^4 + bx^2 + c also nur mit geraden Exponenten, wegen Symmetrie.
Nullstelle bei x = 2
f(x=2) = a2^4 + b2^2 + c = 16a + 4b + c = 0
Hochpunkt bei H(1|9)
f(x=1) = a + b + c = 9
f'(x) = 4ax^3 + 2bx
f'(x=1) = 4a + 2b = 0
Dann kann man lösen...
16a + 4b + c = 0
a + b + c = 9
4a + 2b = 0
--------------
1. Gleichung minus 2. Gleichung
15a + 3b = -9
3. Gleichung * 1,5
6a + 3b = 0
3b = -6a
Einsetzen in vorherige Gleichung
15a - 6a = - 9
daraus folgt a = -1
Das eingesetzt in 3b = -6a
ergibt 3b = 6 ergibt b = 2
Nehme ich diese Gleichung a + b + c = 9 und setze ein:
-1 + 2 + c = 9
c = 8
Damit lautet die Funktion
f(x) = -x^4 +2bx² + 8
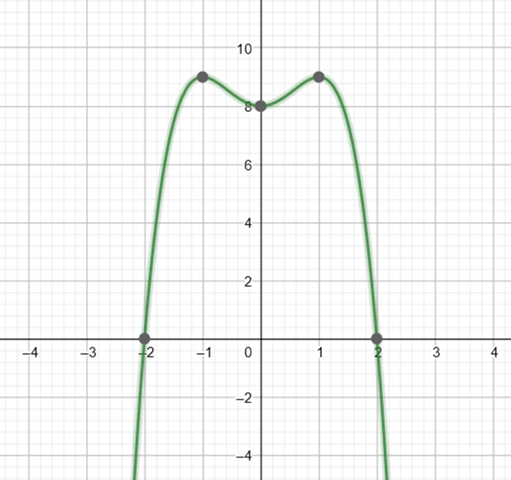
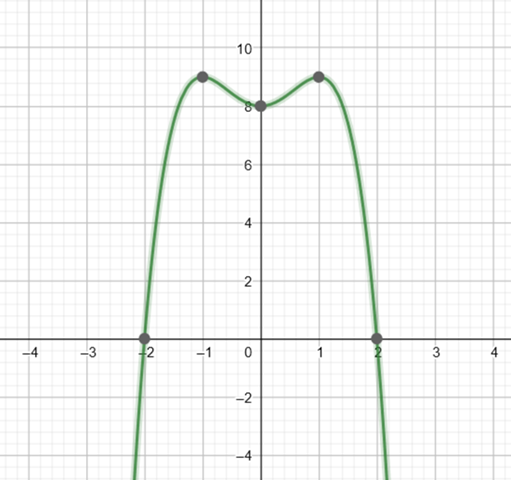
Hochpunkt bei 1|9
Achsensymmetrisch
Nullstelle bei x = 2
Das sieht doch gut aus.
Da brauchst du nicht die Ableitung, eine Nullstelle heißt ja nichts anderes als
bei dem Hochpunkt musst du aber die erste Ableitung an der Stelle Null setzen
außerdem weißt du dass es sich um einen Hochpunkt handelt, daher hast du noch die Bedingung