Mathe, Maßstäbliche Vergrößerung?
Hallo,
und zwar verstehe ich dieses Thema in Mathe nicht (9.Klasse) :
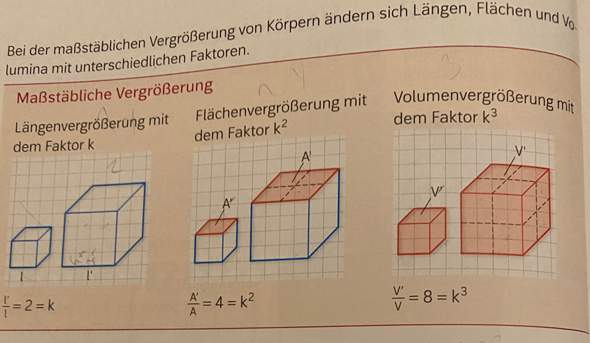
Wenn es stattdessen nicht der 1cm Würfel sondern ein 2cm Würfel wäre und der k Wert 2,5 wäre, wäre dann die Längenvergrößerung 5, die Flächenvergrößerung 6,25 und die Volumenvergrößerung 15,625 oder habe ich das Thema falsch verstanden?
In dem Buch ist noch eine erklärung die mich dann komplett verwirrt hat:
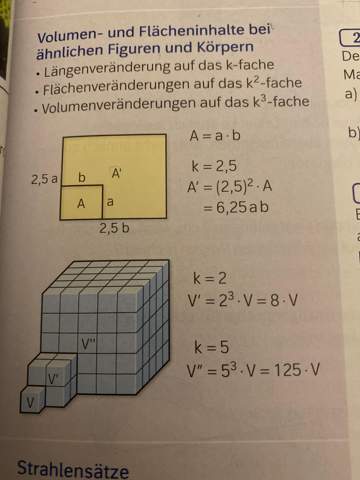
Kann mir jemand das Thema erklären, Anhand meines Beispiels?
Mit freundlichen Grüßen JuergenBaum
4 Antworten
Das heisst der Würfel A muss nicht so viel wie das Volumen in den Würfel A‘ reinpassen?
Ich verstehe was der k-Faktor bedeutet, aber es ist nicht so einfach vorstellbar. Ich würde mir immer Beispiele machen.
- Eine Seite von z.B. a = 3 cm wäre bei einem doppelt so großen Würfel 2a = 6cm. (Hier ist k = 2, da 6/3 =2.
- Eine Fläche von a*a = 3cm * 3cm = 9cm² hätte bei doppelt so großer Seitenlänge 2a * 2a = 3 cm * 3cm = 2*3cm * 2*3cm = 36 cm². Hier wäre k² = 36/9 = 4 und k = 2
- Bei einem Volumen von a*a*a = 3 cm * 3cm * 3cm = 27 cm³ hätte ein Würfel mit doppelt so großer Seitenlänge a das Volumen von 2a*2a*2a = 8a = 8*3³ = 216 cm³. Hier wäre k³ = 216 / 27 = 8 und k = 2
-------------------------
Das gleiche nochmal mit einem 1,5 mal so großen Würfel.
- Eine Seite von z.B. a = 3 cm wäre bei einem 1,5x so großen Würfel 1,5a = 4,5cm lang. Hier ist k = 1,5 da 4,5/3 =1,5.
- Eine Fläche von a*a = 3cm * 3cm = 9cm² hätte bei 1,5x so großer Seitenlänge 1,5a * 1,5a = 1,5²*(3cm)² = 20,25 cm². Hier wäre k² = 20,25/9 = 2,25 und k = 1,5
- Bei einem Volumen von a*a*a = 3 cm * 3cm * 3cm = 27 cm³ hätte ein Würfel mit 1,5 fach so großer Seitenlänge a das Volumen von 1,5a*1,5a*1,5a = 3,375a³ = 3,375*3³ cm³= 4,5³ cm³ = 91,125 cm³. Hier wäre k³ = 91,125/ 27 = 3,375 und k = 1,5
Bei eine Länge ist k^1 bei einer Fläche ist k² und bei einem Volumen ist k³.
Probe:
Bei deinem Beispiel einen Würfel mit der Kantenlänge 2cm um den k-Wert 2,5 zu vergrößern, kommst du bei der Kantenlänge auf 2,5*2cm = 5cm.
Die Fläche einer Würfelseite berechnest du mit 5cm*5cm = 25cm^2 oder eben mit 2,5*2cm * 2,5*2cm = 2,5^2 * (2cm)^2 = 6,25*4cm^2 = 25cm^2.
Das Volumen mit 25cm^2 * 5cm = 125cm^3 oder eben 2,5*2cm * 2,5*2cm * 2,5*2cm = 2,5^3 * (2cm)^3 = 15,625*8cm^3 = 125cm^3.
Allgemein gilt für einen Würfel den du mit k vergrößerst also a'= k*a wobei a' die vergrößerte und a die ursprüngliche Kantenlänge ist.
Für die vergrößerte Fläche gilt also A'= k^2 * a^2 und das Volumen V'= k^3 * a^3
Ich hoffe du hast es damit verstanden.
Danke, 2 Tage vor Arbeit hast du mein Leben gerettet!
Du hast richtig gedacht:
Seitenlänge a=2cm und Faktor k=2,5:
Seitenlänge = a • k = 2cm • 2,5 = 5 cm
Fläche = (a • k)² = a² • k² = 4cm² • 6,25 = 25cm²
Volumen = (a • k)³ = a³ • k³ = 8cm³ • 15,625 = 125cm³
Aber in der Schule hatten wir als Beispiel das der Würfel A 8 mal in den Würfel A‘ reinpasst und der 2cm Würfel passt doch nicht 125 mal in den Würfel A‘ , das müssten doch 15,625 ergeben, weil der Würfel A‘ ungerade vergrößert wurde.
Dann wat das Beispiel in der Schule mit einem k-Faktor von 2, denn dann hast du beim Volumen V'= 2^3 * a^3
Und weil 2^3 = 8 passt er eben 8mal rein.
Es kommt also auf den k-Faktor an.
Das heisst der Würfel A muss nicht so viel wie das Volumen in den Würfel A‘ reinpassen?
Einfache Erklärung mit 1cm:
die Seitenlänge verdoppelt sich: 2cm
die Fläche ver4facht sich: 4cm^2
dss Volumen ver8fscht sich: 8^3
Könntest du mir das anhand meines Beispiels nochmal erklären, ich kriege dad nicht ihn.
Danke!!!