Mathe Funktion Lösung?

Kann jemand bitte helfen
2 Antworten
4a) Die jeweiligen Gleichungen findet man durch Punktproben (wenn man die beiden Punkte einsetzt).
Parabel:
Ansatz:
y = ax^2 + c
Punktprobe mit A:
2 = 16a + c
c = 2 - 16a
Punktprobe mit B:
-1 = 4a + c
c = -1 - 4a
c = c
2 - 16a = -1 - 4a
12a = 3
a = 1/4
c = -1 - 4a = -1 -1 = -2
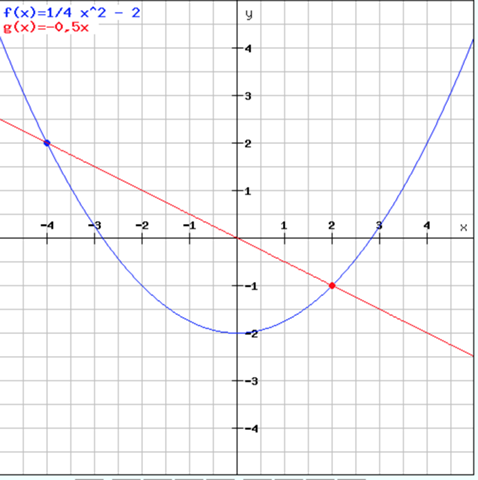
p: y = 1/4 x^2 - 2
So macht man das auch mit der Geraden:
Ansatz:
y = mx + b
und erhält dann:
g: y = -0,5x
Um die Parabel zu zeichnen, braucht man eine Wertetabelle:

Die Gerade legt man einfach durch die beiden Punkte:

b)
Für die Steigung von senkrechnten Geraden gilt:
m1 * m2 = -1
m2 = -1/m1 = -1/-0,5 = 2
Ansatz:
h: y = 2x + c
Punktprobe mit S(0/-2):
-2 = 0 + c
c = -2
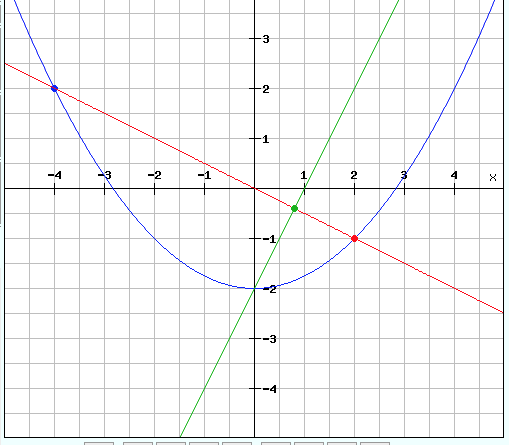
h: y = 2x -2
Berechnung Schnittpunkt:
Für T gilt: der y-Wert muss derselbe sein, daher Ansatz:
y = y
-0,5x = 2x -2
2,5x = 2
x = 2/2,5 = 4/5 = 0,8
y = 2x -2 = 1,6 - 2 = -0,4
Damit:
T(0,8 / -0,4)
Spasseshalber, aber in der Aufgabe nicht gefordert:


Parabel:
p(x) = ax² + c
Bilde jeweils eine Gleichung mit A und mit B und bestimme in diesem Gleichungssystem die Werte für a und c.
Gerade:
g(x) = m * x + b
Bilde jeweils eine Gleichung mit A und mit B und bestimme in diesem Gleichungssystem die Werte für m und b.
Die Orthogonale zu g hat die Steigung m_1 = -1 / m.
Setze in die Funktionsgleichung h(x) = m_1 * x + d die Koordinaten des Scheitelpunktes ein (dieser liegt auf der y-Achse) und bestimme die Werte für d.
Setze g(x) und h(x) gleich und bestimme die Koordinaten von Schnittpunkt T.
p(x) = ax² + c
A ( -4│2) einsetzen:
(1) 2 = a * (-4)² + c
B (2│-1) einsetzen:
(2) -1 = a * 2² + c
-----------------------
(1) 2 = a * (-4)² + c
(2) -1 = a * 2² + c
-----------------------
2 - a * (-4)² = -1 - a * 2²
2 - 16 * a = -1 - 4 * a
12 * a = 3
a = 1/4
2 = (1/4) * (-4)² + c
c = -2
p(x) = (1/4) * x² - 2
danke für die Antwort jedoch kapier ich nicht wie ich eine Gleichung aufstellen soll wenn ich nur 2 Werte gegeben habe