Mathe Aufgabe stochastik dringen Hilfe?
https://www.mathelounge.de/88565/wahrscheinlichkeitsverteilung-spieler-zehnfache-augensumme
ich hoffe es ist möglich dadraus zuzugreifen.
ich versteh nicht, wie man auf die Tabelle kommt da brauch ich dringend eine Erklärung wie kommt man auf 1/36, 2/36 usw
1 Antwort
Hallo Tura27,
die Ergebnismenge ist hier Ω = {(x, y): x, y ∈ {1, ..., 6}}, also die geordneten Paare (x, y), wobei x und y die Augenzahlen des ersten bzw. zweiten Würfels sind.
Für z ∈ {2,..., 12) schreiben wir {x + y = z} = {(x, y) ∈ Ω: x + y = z}, also das Ereignis, dass die Augensumme z ist besteht aus den geordneten Paaren (x, y), sodass x + y = z. Beispiel: A = {"Augensumme ist 4"} = {(1, 3), (2, 2), (3, 1)}.
Die Wahrscheinlichkeit ist für jedes mögliche Paar dieselbe. Weil es insgesamt 6 ⋅ 6 = 36 Paare sind, ist also die Wahrscheinlichkeit für ein einzelnes mögliches Augenzahlenpaar (x, y) ∈ Ω: P({(x, y)}) = 1/36. Die Wahrscheinlichkeit von einem Ereignis berechnet man bei solchen Laplace-Experimenten, indem man die Anzahl der günstigen Elemente durch die Anzahl aller möglichen Elemente addiert. Die Anzahl aller möglichen Elemente ist |Ω| = 36. Die Anzahl der günstigen Elemente ist die Anzahl der Elemente, die sich in dem Ereignis befinden, dessen Wahrscheinlichkeit wir berechnen wollen. In unserem Beispiel: |A| = |{"Augensumme ist 4"}| = |{(1, 3), (2, 2), (3, 1)}| = 3. Also ist P(A) = 3/36 = 1/12.
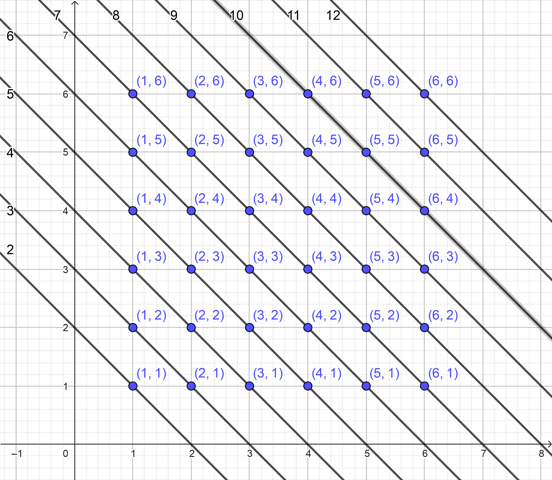
Man kann das ganze ganze graphisch so darstellen:
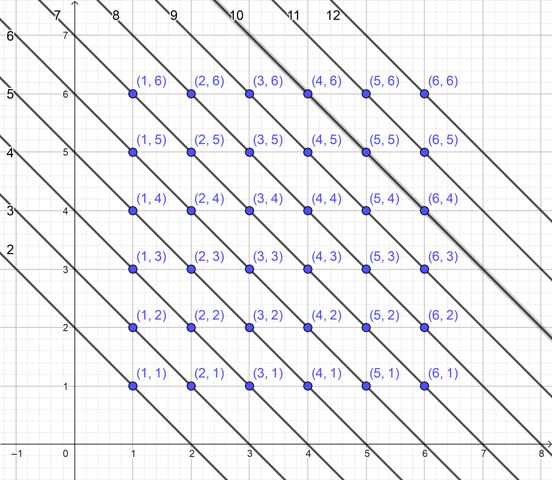
Alle Zahlenpaare, die dieselbe Summe ergeben, befinden sich auf einer Gerade. Die Wahrscheinlichkeit für eine bestimmte Augensumme ist der Anteil der Punkte, der sich auf dieser Geraden befindet. Wenn man von links unten anfängt, kommt man genau auf die Zahlen 1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1 und das jeweils durch 36, weil es insgesamt 36 Punkte sind.