Mathe Aufgabe falsch gemacht?
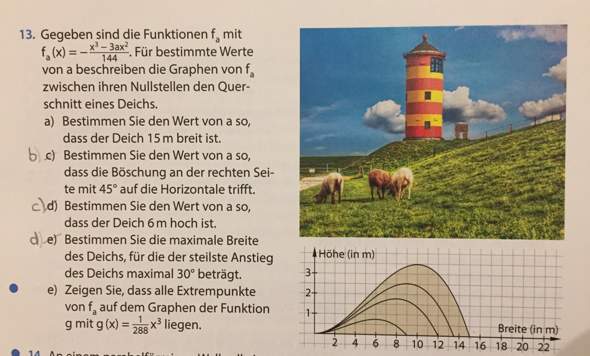
Aufgabe a) habe ich hinbekommen, aber die restlichen Aufgaben wie b-d ging überhaupt gar nicht. Bei b) kam ein Wert raus, welches zu groß ist und bei c) war es mit Cosinus. Kann mir jemand die Aufgabe erklären?
2 Antworten
f(x) = (x³ - 3ax²)/(-144)
.
b)
erstmal die Nullstellen bestimmen ( 0 und 3a )
.
f'(x) = 1/48 (2 a - x) x
muss -1 sein bei 3a, der Nullstelle ganz rechts (arctan(-1) = 45°)
.
1/48*(2a*3a -(3a)²) = -1
( 2a*3a - (3a)² ) = -48
6a² - 9a² = -48
a² = -48/-3 = +16
.
.
c)
f(Extremwert) soll 6 sein
.
0 = 1/48 (2 a - x) x
entweder bei 0 oder bei 2a
.
6 = ((2a)³ - 3a(2a)²)/(-144)
a auch 6
.
.
d)
zweite Ableitung = 0
(a ist Lös)
.
tan(30) = 1/wurzel(3)
.
1/48 (2 a - a) a = 1/w(3)
.
.
.
.
e)
die Extrema liegen bei
( 2a / (a³/36) )
.
x = 2a >>>> x/2 = a
y = a³/36
.
jetzt für a den Wert x/2 einsetzen
.
y = (x/2)³ / 36
= x³ / 8*36
.
b) 45° bedeutet hier, dass die Steigung an der rechten Nullstelle (bei x=3a) -1 sein muss, also f'(3a)=-1
c) hier rechnest Du aus wo der Hochpunkt (xh) ist und setzt dann f(xh)=6 (wieso Cosinus?)
d) der steilste Anstieg ist am Wendepunkt (xw). Hier soll die Steigung 30° sein, also m=tan(30°)=..., d. h. f'(xw)=m nach a umstellen, die rechte Nullstelle von diesem fa gibt dann die Breite des Deichs an
im TR ? cos könnte höchstens im Zusammenhang mit den komplexen Wurzeln auftauchen , aber die 6 sollte auch dabei sein bei den Lösungen
Könnten Sie mir vielleicht ein Foto schicken?
wovon ? im Kommentar ist ein Link ! ( hellblau unterlegt )
Warum soll denn bei einer ganzrationalen Funktion eine Lösung mit Cosinus rauskommen, wenn man das "ganz normal" mit den üblichen Äquivalenzumformungen löst? Das zeigt, dass Hilfsmittel nicht "bedingungslos" hilfreich sind (vor allem, wenn diese (wie hier) den Bereich der reellen Zahlen verlassen...)
Ich habe die Funktionsgleichung bei c) gleich 6 gesetzt, aber da kam etwas mit Cosinus raus