Kommt es zu einer Kollision?

Das Schnittwinkelproblem

Ich weiß, das a) falsch ist, könntet ihr mir vielleicht die ganze Aufgabe a genaustens erklären mit lösungsweg? 🥺 Das wäre mega nett!

Answer 1

[Hamburger02]

f(x) = 1/4 x^2 - x + 2
g(x) = 2x - 6

a) Grahische Lösung: es knallt

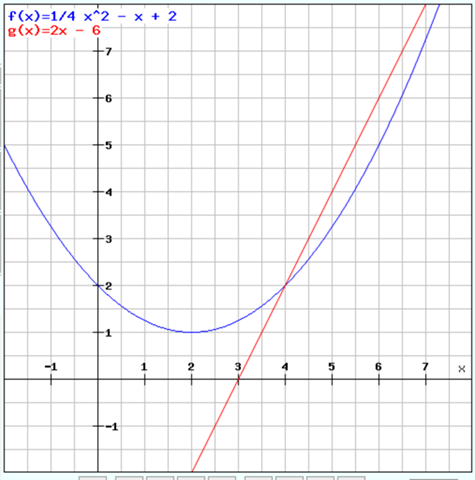
Rechnerische Lösung:

Es muss ein Schnittpunkt gefunden werden, indem man f(x) und g(x) gleichsetzt:
1/4 x^2 - x + 2 = 2x - 6

Da machen wir eine quadratische Löung draus und lösen die dann:
1/4 x^2 - 3x + 8 = 0
Damit die pq-Formel funxt, multiplizieren wir mit 4, damit das x^2 frei steht:
x^2 - 12 x + 32 = 0

Deine Lösung ist also richtig. Bei 8 würde er wieder aus der Kaimauer rauskommen und das Wasser erreichen. Es knallt aber schon beim ersten Schnittpunkt, also bei
x = 4

Um den Einschlagswinkel zu ermitteln, müssen wir beide Funktionen ableiten und dann den jeweiligen Wert an der Stele x = 4, welches ja die Steigung ist, ausrechnen:

f(x) = 1/4 x^2 - x + 2
f'(x) = 1/2x -1
f'(4) = 1

g(x) = 2x - 6
g'(x) = 2

Nun müssen wir aus den beiden Steigungen den Winkel dazwischen ausrechnen. Das geht über das Steigungsdreick, indem wir zunächst den Winkel zur x-Achse ausrechnen:
tan α = Δy/Δx = f' = 1
α = arctan1 = 45°

tan β = g' = 2
β = arctanβ 2 = 63,4°

Schnittwinkel γ = β - α = 63,4° - 45° = 18,4°

Answer 2

[frankfurt1000]

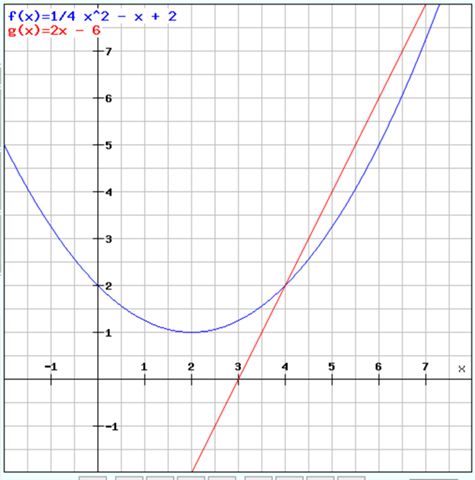
a) Du hast es bereits rausbekommen. Die beiden Kurven schneiden sich bei $x=4$ und $x=8$ also kommt es an den Stellen zu einer Kollision.

b)
Hier musst du den Schnittwinkel berechnen. Um den Schnittwinkel zu bestimmen, brauchen wir die Steigung.
1. Punkt: $f'\left(x\right)=\frac{x}{2}-1$ $g'\left(x\right)=2$ Setze ersten Punkt ein, um die Steigung zu kriegen: $f'\left(4\right)=\frac{4}{2}-1=2-1=1=m_1$ $g'\left(4\right)=2=m_2$ Setze in Formel für Schnittwinkel ein: $\tan\left(alpha\right)=\ \left|\frac{m_1-m_2}{1+m_1\cdot m_2}\right|=\left|\frac{\left(1-2\right)}{1+1\cdot2}\right|=\left|-\frac{1}{1+2}\right|=\left|-\frac{1}{3}\right|=\frac{1}{3}$ Also ist: $\arctan\left(\frac{1}{3}\right)=alpha$ $alpha\approx18,43Grad$ Das Gleiche mit dem zweiten Punkt: $f'\left(8\right)=\frac{8}{2}-1=4-1=3=m_1$ $g'\left(8\right)=2=m_2$ $\tan\left(alpha\right)=\left|\frac{m_1-m_2}{1+m_1\cdot m_2}\right|=\left|\frac{3-2}{1+3\cdot2}\right|=\left|\frac{1}{1+6}\right|=\left|\frac{1}{7}\right|=\frac{1}{7}$ $\arctan\left(\frac{1}{7}\right)=alpha$ $alpha\ \approx8,13Grad$

Woher ich das weiß: Studium / Ausbildung – Jahrgangsbester der Abschlussklasse und aktuell Mathestudium

Answer 3

[f0felix]

Bei a) SP sind bei x=4 und x=8, das ist richtig;

da der Fahrer erst bei x=4 ist, trifft er hier auf die Mauer

b) Winkel zwischen der Geraden und der Tangente an dem Graphen bei x=4 bestimmen

m=f’(4)

dann den Schnittwinkel zwischen zwei Geraden berechnen...

Woher ich das weiß: Studium / Ausbildung

Comments

[f0felix]

Es könnte auch sein, dass der Fahrer von rechts kommt, da in der Aufgabenstellung nichts weiter angegeben ist...

Answer 4

[SevenOfNein]

Wieso denkst Du, dass a) falsch ist?

Für die beiden (x) - Werte kommt bei beiden Funktionen der gleiche y - raus. Also da schneiden sich die Funktionsgraphen. Das Boot fährt gegen die Mauer. Je nachdem von wo es losfährt, bei Punkt 1 oder 2.