Kleiner Stein im Reifen?
Ein Auto fährt mit 120kmh. Ein im Reifen verklemmter kleiner Stein löst sich aus dem Profil, als sich der Reifen gerade nach oben bewegt. Welche Geschwindigkeit (Betrag und Richtung) hat der Stein für einen außen stehenden Beobachter direkt nach dem Loslösen vom Reifen?
Richtung:
Also wenn es gerade nach oben geht müsste der Stein doch nach oben fliegen, da ja die Geschwindigkeit tangential zur Kreisbahn ist. Die soll allerdings laut Lösung nach vorne fliegen.
Geschwindigkeit
Ich dachte, dass der Stein die gleiche Geschwindigkeit, wie der Reifen hat, da die Geschwindigkeit ja wie gesagt tangential zur Kreisbahn ist, plus die Geschwindigkeit des Autos. Die Lösung ist aber 170 km/h mit der Begründung, dass er im 45° Winkel wegfliegt.. Aber wieso?
5 Antworten
120km/h : cos(45) = 170km/h
da der Stein im Winkel von 45 Grad fliegt, kann man mit einem Geschwindigkeitparallelogramm die Beträge der Geschwindigkeiten "oben" (vertikal) und "rechts" (horizontal) bestimmen.
Danke ich hätte da noch eine Frage, das Bild dazu werde ich hier nochmal posten .. Und zwar: Wenn der Stein oben ist, dann fliegt der Stein waagerecht nach vorne (was ich mittlerweile denke ich auch verstehe), wenn jetzt der Stein unten ist, würde der dann gar nicht wegfliegen, da der Geschwindigkeitsvektor des Steins und des Autos in verschiedene Richtungen zeigen?
Betragsmäßig ist v gleich groß, auch wenn die Richtungen anders sind. Bei einer Kreisbewegung ist v an jeder Steller gleich, ich hoffe ich darf das so sagen :D, wenn Reibung mitspielt, ist es anders!
wenn jetzt der Stein unten ist, würde der dann gar nicht wegfliegen
Korrekt! Fällt der Stein ab, während er auf der Straße liegt, dann hat er die gleiche Geschwindigkeit wie die Straße (falls der Reifen nicht rutscht).
Der Stein würde also einfach liegen bleiben.
Noch nicht ganz verstanden :D Fliegt der Stein jetzt weg oder nicht? :D
Die Frage ist gerade, wieso er im 45° Winkel wegfliegt?
an welchem Punkt löst er sich 180° Möglichkeit hätte er ja bei deinen schwammigen Angaben
weil der stein nach oben fliegt und die erdanziehungskraft mitwirkt
Salue
Erstmal, meine Versicherung musste mir schon 2xMal eine neue Frontscheibe bezahlen. Ich lebe hier in einen Kiesabbaugebiet und die entgegenkommenden LW haben des Öfteren Steine im Profil eingeklemmt.
Der Stein wird ja beim Überrollen bewegt und kann sich durch das Walken früher oder später aus dem Profil herausarbeiten. Prinzipiell kann er in alle Richtungen, ausser nach unten, davonfliegen. In den meisten Fällen fliegt er an den Kotflügel, oder direkt nach vorne oder hinten.
Nur wenn das Vorderrad leicht eingelenkt ist, ist die "freie" Schussrichtung nicht überdeckt. Meine Frontscheiben haben Ihren Tod immer in leichten, schnell zu fahrenden, Kurven gefunden.
Der Stein verlässt seine Einklemmung mit derselben Geschwindigkeit, mit der das Fahrzeug fährt. Also z.B. mit 80 km/h.
Nur, vergiss nicht, ein solches Projektil kann schon mal 10 Gramm schwer sein und es ist scharfkantig. Persönlich bin ich deshalb sehr dankbar dafür, das nicht mein Gesicht, sondern die dreischichtige Frontscheibe diesen "Stunt" übernommen hat.
Es grüsst Dich
Tellensohn
hab mal eine schwammige zeichnung gemacht,
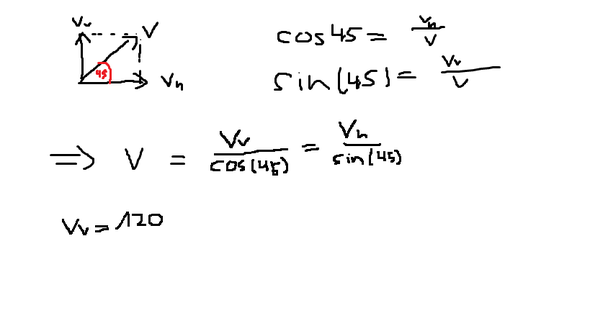
Vielen Dank! :) Also hat man einen 45° Winkel, da die vertikale Komponente gleich der horizontalen Komponente ist? Kommt die vertikale durch das Auto und die horizontale durch die Geschwindigkeit des Steines oder wieso sind beide gleich?
Gerade hier ist es ein Spezialfall und der winkel ist 45 Grad.
Bei anderen Aufgabentypen ist es genau umgekehrt: da ist die Anfangsgeschwindigkeit und der Startwinkel gegeben.
Ja aber tritt der Spezialfall gerade daher auf, weil die vertikale und horizontale Komponente gleich sind?
korrekt!
Superpositionsprinzip:
a) Bewegung nach oben - also bewegt sich der Stein mit 120 km/h nach oben
b) Rad bewegt sich mit 120 km/h nach vorn - Stein also auch - also 120 km/h waagerecht
nun die Addition der beiden Geschwindigkeiten: Wurzel aus 120² + 120² = 169,8 km/h im 45° Winkel nach oben in Bewegungsrichtung.
Das könnte sogar klappen, da der Reifen ja "aus dem Weg" "rollt" ;-)
Für genauere Angaben müsste man die Reifendimensionen kennen und die Abrollkurve bestimmen:
http://mathenexus.zum.de/CAS_inf/abrollen_Kreis_Elli_Aussen.html