Kann mir jemand helfen?
Angenommen, die Weltbevölkerung vermehrt sich nach der Formel N(t)=N0*e^(λ*t). 1960 gab es ca. 3 Mrd. Menschen, 1995 ca. 5,6 Mrd.
a) Bestimme die Konstante λ!
b) Wann wird die Erde 15 Mrd. Einwohner haben, wenn die Bevölkerung im selben Tempo weiterwächst?
Kann mir bitte jemand helfen? Ich komme nicht weiter...
2 Antworten
5.6/3 = e^(L*35)............ln
ln(5.6/3) = L*35
ln(5.6/3)/35 = L = 0.01783
.
.
15 = 3e^(0.01783*t)...durch 3 und ln
5 = 0.01783t
5/0.01783 = t = ?
Es wird dir zwar nicht viel helfen, aber ich könnte dir b) ausrechnen, ohne diese komische Formel.
Mithilfe des Zinseszins:
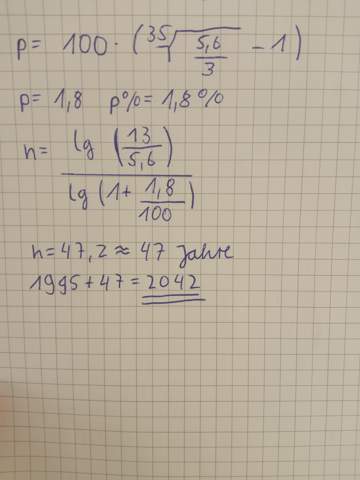
Die Bevölkerung wird also im Jahr 2042 (wenn sie in diesem Tempo weiter wächst) die 15 Mrd Einwohner knacken.
Tut mir leid, dass ich dir leider nicht anderweitig weiterhelfen kann.
LG
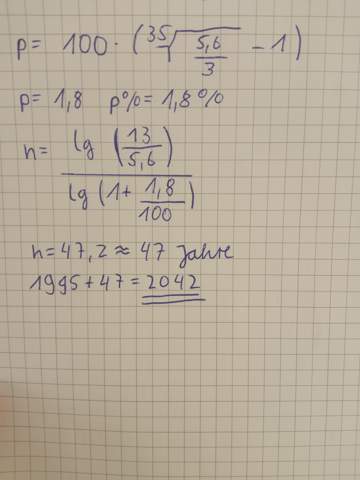
Bin erst in der 8. Klasse, weshalb wir das Thema leider noch nicht hatten.
P ist bei mir 1,79929, da kann man doch auf 1,8 aufrunden oder nicht?
normal ja , aber hier geht es um Fortschreibung von Einwohnerzahlen . Und wie bei der Bank : Jeder Euro und Cent zählt.
ich habe anderen Wert , aber das liegt an unterschiedlichen Rechnern.
ich käme auf 90.2657, du auf 89.41 Jahre
so um 2050 rum also .
Basisjahr ist 1960 nicht 1995 .
bei dir steht 13 . Du meinst 15 ?
.
Ansatz nicht verkehrt und Lösung richtig . In der Schule evtl anderer Weg gewünscht.
.
ach ja, man sollte sich hier ruhig ein paar Stellen mehr hinter dem Komma gönnen bei p