kann mir jemand die unten angegebene postulate und axiome von euklid erklären,gerne mit beispiel wo es geht?
- Was demselben gleich ist, ist auch einander gleich.
- Wenn Gleichem Gleiches hinzugefügt wird, sind die Summen gleich.
- Wenn von Gleichem Gleiches weggenommen wird, sind die Reste gleich.
- Was miteinander zur Deckung gebracht werden kann, ist einander gleich.
- dass man eine begrenzte gerade Linie zusammenhängend gerade verlängern könne,
- dass, wenn eine gerade Linie beim Schnitt mit zwei geraden Linien bewirke, dass innen auf derselben Seite entstehende Winkel zusammen kleiner als zwei rechte würden, dann die zwei geraden Linien bei Verlängerung ins Unendliche sich treffen würden auf der Seite, auf der die Winkel lägen, die zusammen kleiner als zwei rechte seien (kurz: dass zu einer geraden Linie durch einen gegebenen Punkt, der außerhalb dieser Geraden läge, höchstens eine dazu parallele gerade Linie existieren dürfe
3 Antworten
1. Wenn a=b und b=c dann ist auch a=c
2. Wenn a=b dann ist auch a+c = b+c
3. Wenn a=b dann ist auch a-c=b-c
4. Wenn du zwei Formen, zB Dreiecke deckend übereinander legen kannst, sind sie gleich in ihren Dimensionen.
5. Man kann halt eine Gerade Linie durch eine weitere Linie die sich abschließt erweitern.(?)
6. Dies besagt in moderner Formulierung, dass es zu jeder Geraden g und jedem Punkt P nicht mehr als eine Parallele zu g durch P geben kann.
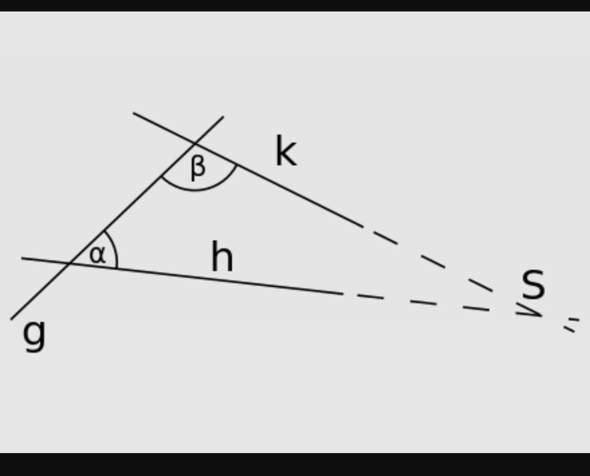
Hier die ursprüngliche Aussage bildlich: wenn g h und k schneidet und Alpha und Beta kleiner als 90° sind schneiden sich h und k irgendwann.

Weiß jetzt nicht, was die Euklidische Geometrie ist, aber ich stelle mir die Axiome, die ich irgendwie verstehe, so vor. Ich hoffe du kannst das dann irgendwie auf die Euklidische Geometrie übertragen:
Wenn Gleichem Gleiches hinzugefügt wird, sind die Summen gleich.: Sagen wir wir haben zwei mal eine 4 (beide Gleich), nun wird beiden Gleiches hinzugefügt (2). So wird auch das Ergebnis gleich sein: 4+2=6
4+2=6
Ich könnte mir auch vorstellen, dass gemeint ist: wenn wir bspw. 2 und 4 gegeben haben und nun 3 anfügen. Dann wären die Ergebnisse zwar nicht die selben, aber gleich. Denn zwischen 2 und 4 ist eine Differenz von 2 und ziwschen 5 und 7.
Wenn von Gleichem Gleiches weggenommen wird, sind die Reste gleich.:
Umgekerte Logik von oben
Was demselben gleich ist, ist auch einander gleich.:
Das verstehe uch nicht ganz, vorstellen tue ich mir aber folgendes:
Wenn wir 3 und 9 haben. Und nun eine dritte Zahl ins Spiel kommt: 6 dann vergleicht man bspw. 3 mit 6 und stellt fest, dass 6 sowie 3 durch 3 teilbar sind, so muss, weil 3, dass gleiche wie 9 in dem Fall, auch 9 automatisch durch 3 teilbar sein.
Den Rest begreife ich nicht ganz. Hoffe konnte dir irgendwie helfen. 🤷🏼♂️
das erste kann ich sogar
Weil x = a und auch y = a , gilt x=y
Wenn Trick 110 cm ist und Track auch 110 cm , dann ist Trick so groß wie Track
.
.