Kann mir jemand die b) rechnen?

3 Antworten
Es müsste zwei t1 und t2 geben, so dass
e^(t1*x) = e^(t2*x)
ist, also (t1*x) = (t2*x)
Damit ist t1 = t2 und x = 0 ist der einzige gemeinsame Punkt.
Bevor die Gleichung durch (x+5) geteilt wird, hält man fest (hält man das nicht vor der Division fest, "verliert" man eine Lösung).
Es bleibt:
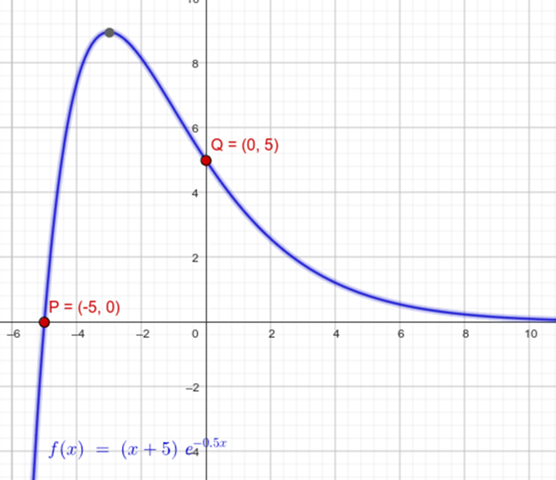
Die Scharfunktionen haben also die gemeinsamen Punkte P(-5 | 0) und Q(0 | 5).
Skizze t = -1/2

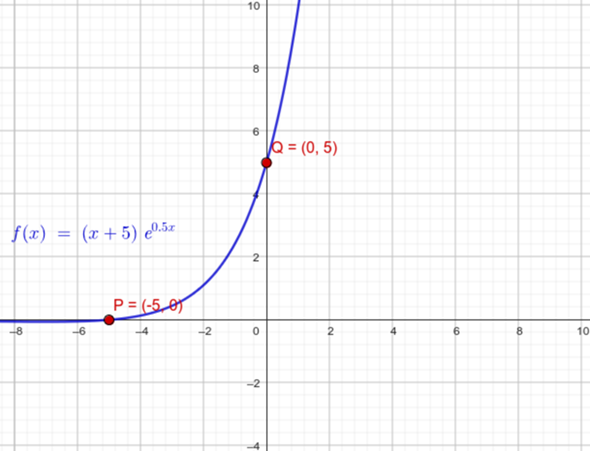
Skizze t = + 1/2

beim Gleichsetzen steht am Rand ein PUNKT . Aber es wird doch geteilt /
Aber es steht auch ein -t2 im Exponenten und kein t2. Daher passt das mit der Multiplikation schon.
ok ok . stimmt . ich wollte schon wieder was anmerken weil ich da eine 2x nach der Multiplikation sah , aber -ax + +ax ist natürlich Null
... tja manchmal kann ich gannssss rafiniert plutimizieren ;-)
Du hast die 2 vor der Klammmer übersehen bei Aufgabe b.)
Deshalb ist einer deiner Punkte nicht korrekt.
Wenn x = 0 ist, dann ist der Wert von t vollkommen egal, weil in dem Fall das Produkt t * x immer denselben Zahlenwert annimmt, nämlich Null, völlig unabhängig davon welchen Wert t hat.
Der Punkt lautet (0 | 10)
Wie hast du gerechnet weil ich hab nicht nur x=0 sonder auch x=-5
Ja, du hast recht, x = -5 sollte auch eine Lösung sein, also der Punkt (-5 | 0)
Gerechnet habe ich überhaupt nicht, nur kurz nachgedacht.
Gerne, kannst ja mal nach "Satz vom Nullprodukt" googlen, der kommt hier zum Einsatz.
Du hast die Lösungen zu a) gerechnet bräuchte die für b