Kann mir jemand beim Zuordnen der Graphen helfen?

Moin,

im Anhang ist ein Foto von der Aufgabe und ich habe die Lösungen, aber ich verstehe nicht, wie ich darauf gekommen bin. Kann mir das jemand erklären?
Ich verstehe nur Aufgabe a) nicht. Ich wäre sehr dankbar. Liebe Grüße Anna:)

Answer 1

[verreisterNutzer]

zu a)

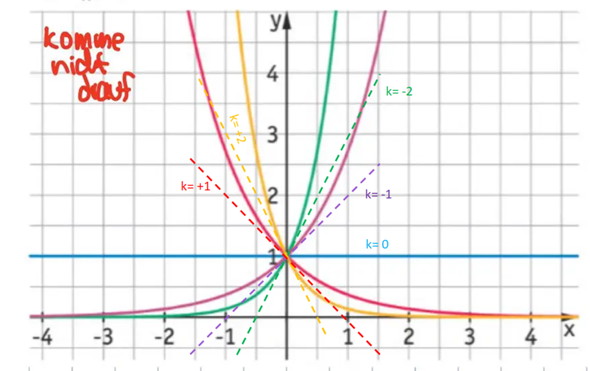
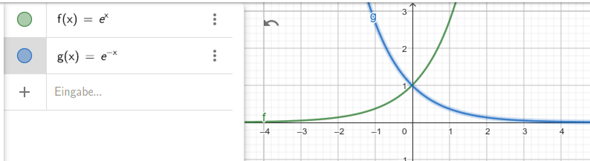
• Die "normale" Exponentialfunktion e^x geht für x -> + ∞ gegen + ∞ und für x -> - ∞ gegen 0. Ein negatives Vorzeichen im Exponenten (e^-x) dreht das Verhalten gerade um: für x -> + ∞ gegen 0 und für x -> - ∞ gegen + ∞. Skizze dazu:
• Nun steht da "-k" als Faktor im Exponenten, daher wird -k positiv, wenn k negativ ist und dann sieht die Exponentialfunktion für k= -2 und k=-1 doch wieder aus wie die "normale" Exponentialfunktion e^x
• Für k=1,2 ist der Faktor im Exponent negativ und die Funktion sieht grundsätzlich aus wie die e^-x
• Der Betrag von k bestimmt die "Steilheit" oder das "Gefälle" (von links nach rechts)
• Für den Wert k=0 ergibt sich e⁰ = 1

Skizze:

Comments

[Martinamey]

Danke! Das schätze ich sehr wert.

Answer 2

[ProfFrink]

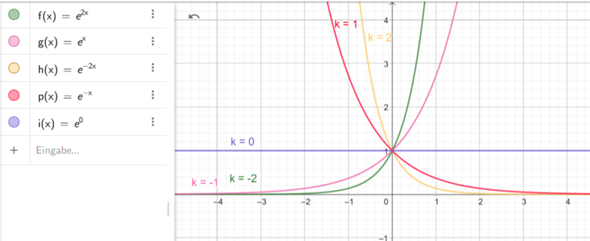
Du betrachtest die parametrisierte Funktion

$f_k\left(x\right)=e^{-kx}$ deren bunte Verläufe Du sehen kannst. Um sie zu unterscheiden schaust Du Dir einfach die Steigung der Kurven an der Stelle x=0 an. Aber zuerst rechnen wir die Steigung in diesem speziellen Punkt aus.

$f'_k\left(x\right)=-k\cdot e^{-kx}$

Und in der Stelle x=0 erwarten wir dann folgende Steigungen

$f'_k\left(0\right)=-k$

Als nächstes zeichnest Du einfach die Tangenten der Kurven immer an der Stelle x=0 mit dem Lineal ein. Du erkennst dann ganz schnell, ob sie die Steigung -2, -1, 0, 1 oder 2 haben. Musst einfach die Kästchen auszählen. Aber Vorsicht: Hier gilt Vorzeichenumkehr. Eine Steigung des Wertes 2 muss nun k=-2 zugeordnet werden usw.

Woher ich das weiß: Studium / Ausbildung

Comments

[Martinamey]

Danke, deine Mühe schätze ich wert!