Kann mir jemand bei der Matheaufgaben zur Tangente helfen?

Hallo,

ich verzweifle gerade an meiner Matheaufgaben (12. Klasse Gymnasium) und würde mich über eine detaillierte Lösung sehr freuen.

Answer 1

[mihisu]

Die Bemerkung [T₄] (bzgl. der Steigung der Normale) ist in der Aufgabe evtl. etwas verwirrend bzw. unpassend. Denn in der Aufgabenstellung geht es nirgends um eine Normale. Die Bemerkung [T₄] kannst du einfach ignorieren, wenn dich das verwirrt haben sollte.

====== a) ======

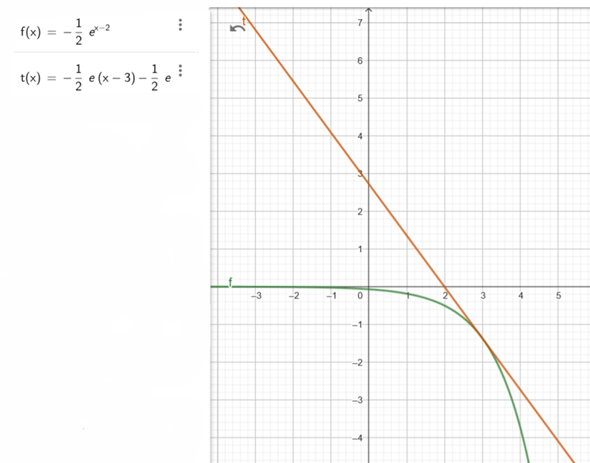
Du solltest den Verlauf einer Exponentialfunktion mit Funktionsterm e^x im Kopf haben. Wegen dem Faktor -1/2 davor ist der Funktionsgraph an der x-Achse gespiegelt und mit Faktor 1/2 in y-Richtung gestaucht. Da x - 2 statt x im Exponenten steht ist der Graph außerdem um 2 Einheiten nach rechts verschoben.

Ich würde für die Skizze insbesondere beachten...

• Der Graph nähert sich für x → -∞ der x-Achse.
• Der Graph fällt mit exponentiellem Verlauf.
• Der Graph verläuft wegen f(2) = -1/2 durch den Punkt (2 | -1/2).

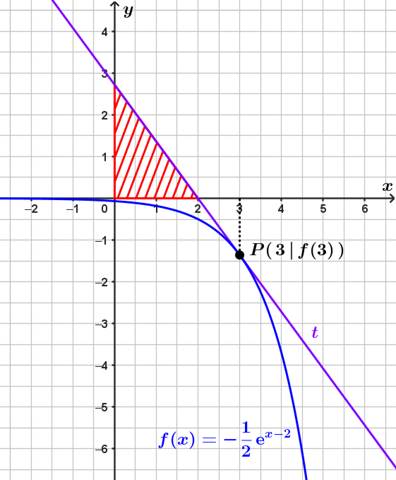
Dann den Punkt P an der Stelle x = 3 markieren und die entsprechende Tangente skizzieren. Dann das entsprechende Dreieck markieren.

====== b) ======

Zunächst einmal wäre es gut, die Gleichung der Tangente zu kennen. Die Steigung der Tangente erhält man mit Hilfe der ersten Ableitung an der entsprechenden Stelle...

$f(x)=-\frac{1}{2}\cdot \text{e}^{x-2}$

$f'(x)=-\frac{1}{2}\cdot \text{e}^{x-2}$

$m_t=f'(3)=-\frac{1}{2}\cdot \text{e}^{3-2}=-\frac{1}{2}\cdot \text{e}^{1}=-\frac{1}{2}\cdot \text{e}$

[Bemerkung: Der Faktor -1/2 bleibt beim Ableiten als konstanter Faktor erhalten. Die Exponentialfunktion ergibt beim Ableiten wieder die Exponentialfunktion, wobei man aufgrund der Kettenregel x - 2 noch nachdifferenzieren müsste, was aber nur einen Faktor 1 liefert, der nichts ändert.]

Für die y-Koordinate des Punktes P erhält man...

$y_P=f(3)=-\frac{1}{2}\cdot \text{e}^{3-2}=-\frac{1}{2}\cdot \text{e}^1=-\frac{1}{2}\cdot \text{e}$

Mit der Steigung und dem Punkt, kann man nun die Gleichung der Tangente aufstellen...

$t:\quad y=m_t\cdot \left(x-x_P\right)+y_P$

$t:\quad y=-\frac{1}{2}\cdot \text{e}\cdot \left(x-3\right)+\left(-\frac{1}{2}\cdot \text{e}\right)$

Da würde ich nun noch -1/2 ⋅ e ausklammern. Das müsste man aber nicht machen.

$t: \quad y=-\frac{1}{2}\cdot \text{e}\cdot \left(x-3+1\right)$

$t: \quad y=-\frac{1}{2}\cdot \text{e}\cdot \left(x-2\right)$

Nun kann man die Schnittpunkte der Tangente t mit den Koordinatenachsen berechnen. Beim Schnittpunkt mit der x-Achse ist die y-Koordinate gleich 0...

$-\frac{1}{2}\cdot \text{e}\cdot \left(x-2\right)=0\quad \Leftrightarrow\quad x-2=0\quad \Leftrightarrow\quad x=2$

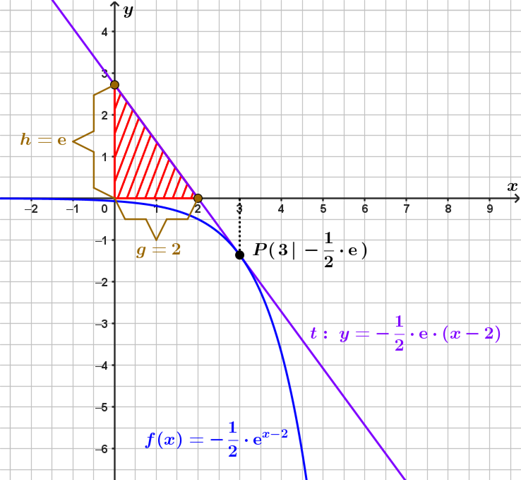
Der entsprechende Schnittpunkt liegt also bei x = 2, sodass die Dreiecksgrundlinienlänge dementsprechend g := 2 beträgt.

Beim Schnittpunkt mit der y-Achse ist die x-Koordinate gleich 0...

$y=-\frac{1}{2}\cdot \text{e}\cdot \underbrace{\left(0-2\right)}_{=-2}=\text{e}$

Dementsprechend beträgt die Dreieckshöhe dann h := e.

Für den Flächeninhalt des Dreiecks erhält man dann...

$A=\frac{1}{2}\cdot g\cdot h=\frac{1}{2}\cdot 2\cdot \text{e}=\text{e}\approx 2\text{,}72$

Der Flächeninhalt des Dreiecks entspricht also der eulerschen Zahl e, welche ungefähr den Wert 2,72 hat.

Comments

[anna3007643]

Vielen, vielen Dank! Ich habe jetzt alles so viel besser verstanden!!

Answer 2

[DerRoll]

a) Erstelle ein Koordinatensystem, erstelle eine Wertetabelle von f und zeichne f in das Koordinatensystem ein. Berechne f'(x). f'(x) ist die Steigung m der Tangente t(x) = m*x + b. Den y-Achsenabschnitt erhältst du wie du es in der 8. Klasse gelernt hast indem du die Gleichung m*3 + b = f(3) nach b auflöst. Nun kannst du auch die Tangente einzeichnen.

b) Die Höhe des in a) benannten Dreiecks ist gerade b, die Länge der zur Höhe gehörende Grundseite ist gleich dem Abstand der Nullstelle von t zum Nullpunkt des Koordinatensystems. Damit kannst du den Flächeninhalt berechnen.

Answer 3

[Gottfried757]

Die 1.Ableitung von f'(x)=-e^(x-3)/2=f(x).

Ermittlung der Tangentengleichung:

g(x)=mx+b

m=f'(3)=-e/2

g(3)=(-e/2) × 3 + b = -e/2

b=e

g(x)=-e/2 × x - e/2

Nullstelle von g(x) ermitteln:

g(x)=0

x=2

Fläche A des Dreiecks ermitteln:

A=1/2 × 2 × b

A = e ~ 2,718

Answer 4

[Rammstein53]

f(x) = -1/2 * e^(x-2)

f'(x) = -1/2 * e^(x-2) (identisch mit f(x))

Die Tangentengleichung von f(x) am Punkt a lautet:

t(x) = f'(a)*(x-a) + f(a)

t(x) =-1/2 * e^(a-2)*(x-a) -1/2 * e^(a-2)

Für a = 3 gilt:

t(x) = -e/2 * (x-3) - e/2

Das Dreieck mit den Koordinatenachsen hat die Basislänge 2 (denn t(2) = 0), und die Höhe

t(0) = -e/2 * (0-3) - e/2 = e

Die Fläche ist dann e*2/2 = e ~ 2.71