Ist ein Körper am Fuße oder auf dem Gipfel eines Berges leichter?
Hallo, ich habe in Physik diese Aufgabe:
Wo trägt ein Forscher seine Ausrüstung leichter, am Fuße oder auf dem Gipfel eines Berges? Begründe.
Meine Antwort lautet: Die Ausrüstung ist auf dem Gipfel leichter, da es dort einen größeren Abstand zur der Erde hat, somit die Anziehungskraft schwächer ist und die Gewichtskraft damit weniger.
Jedoch bin ich mir mit meiner Antwort nicht sicher, und wollte wissen, ob mich jemand korrigieren könnte oder?
Vielen Dank im Vorraus.
4 Antworten
Ich glaube normalerweise solltest du auf dem Berg leichter sein, das ist aber sehr geringer Unterschied.
Allerdings könnte denke ich auch ab einer bestimmten pasenden Masse und Höhe eines Berges die Schwerkraft stärker sein, um aber einzuschätzen ob durchschnittsberge solche Massen mit niedriger Höhe haben fehlt mir zu viel Wissen.
Lg
Wahrscheinlich ist das die gewünschte Antwort. Spürbar ist das aber nicht.
Der Luftdruck ist niedriger, die Gravitation ist immer gleich und nicht mal spürbar. Ausser du bist auf dem Mond.
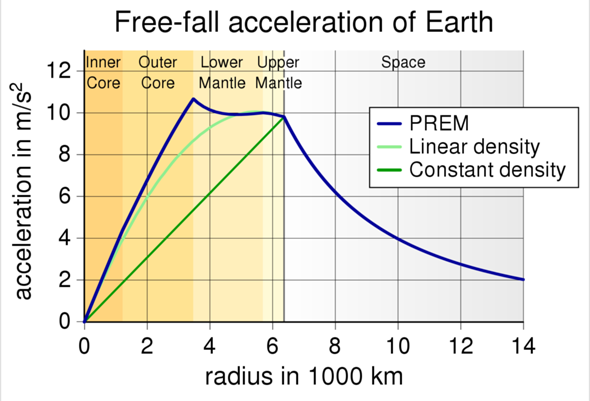
Weil der Erdkern eine größere Dichte als der Mantel hat, sinkt die Schwerkraft, wenn man sich vom Kern entfernt, obwohl man mehr Masse unter sich hat.

Aha...also hat ein größerer Planet eine kleinere Gravitation, weil man weiter vom Mittelpunkt entfernt ist?
Wie kommst du von meiner Aussage zu diesem Schluss? Ich bin verwirrt.
Ich nehme nur Deine Vorgabe auf und spinne sie weiter. Größerer Abstand => kleinere Schwerkraft! Wenn ein Planet größer ist und man steht auf seiner Oberfläche, ist der Abstand zum Mittelpunkt größer, ergo müsste die Schwerkraft kleiner sein!
Meine Aussage ist kein bisschen missverständlich. Wenn du zwei Objekte hast, die Gravitation aufeinander ausüben, und Entfernung zwischen den Objekten steigt, dann sinkt die Gravitation. Was du hier betreibst, ist Wortklauberei, und es ist extrem nervig.
Und Deine Aussage löst nicht die Aufgabe, weil es keine Massepunkte mit irgendeinem Abstand sind! Du könntest das Diagramm anschauen, den Thread-Verlauf durchlesen und zugeben, dass ich Recht hatte und Du Unrecht. Aber die wenigsten können ihren Fehler zugeben, wenn sie ihn überhaupt sehen!
Natürlich kommt es dabei auf die Dichte an! Bei einem homogenen Planeten steigt g mit dem Radius, da die Masse unter den Füßen zunimmt (grüne Linie). Aber da kein Planet homogen aufgebaut ist, ist der Verlauf von g mit dem Radius keine einfacher Verlauf (blaue Linie). Erst steigt g, dann ist es fast konstant, dann sinkt g wieder, sogar innerhalb der Kruste. Kommt noch mehr Kruste dazu, aka ein Berg, sinkt g weiter, aber natl. weniger stark, als wenn dort Luft oder ein Vakuum wäre!
Und nur DANN gilt das GravitationsGesetz von Newton, das Du für soo einfach hältst!
Ok, ich gebe zu, dass es auch etwas mit der Dichte zu tun hat. Ich stehe jedoch zu meiner Position, dass deine beiden Kommentare davor wortklauberisch waren und nichts mit unserem Streitpunkt zu tun haben, der da ist: Auch wenn die Dichte der Erde homogen wäre, wäre die Gravitationskraft auf dem Berg höher als im Tal. Die Dichte des Mantels als Begründung für diese Aufgabe zu verwenden, ist also bestenfalls irreführend.
Das stimmt zwar, aber es kommt auch Teils auf die Masse zur Höhe des Berges an auf dem man steht.
Denn ja, je weiter man sich vom Kern entfernt desto weniger Gravitation ist vorhanden doch ab einer gewissen Masse mehr die eine x Höhe hat kann es doch eigentlich auch sein dass die verlorene Schwerkraft durch die addierte Distanz vom Boden zur Bergspitze kompensiert oder sogar überschritten wird als wie wenn man auf boden wäre?
Ich kenne die Zahlen nicht, aber das hört sich für mich logisch an
Durch den SchichtAufbau der Erde, der eben auch mit DichteUnterschieden einhergeht, steigt die Gravitation vom Zentrum zum Rand des äußeren Kerns an (immerhin flüssiges Eisen), ist dann im Mantel relativ konstant und sinkt dann leicht in der Kruste.
Ja, aber mein Punkt war dass es auch ein Berg sein kann mit soviel x Masse und so wenig x Höhe dass wenn du auf der Bergspitze bist die große Masse des Berges zur relativ kleinen Entfernung der Bergspitze zu Boden du gleich viel bis mehr Schwerkraft erfahren kannst
Diese Behauptung sollte theoretisch auf jeden Fall richtig sein aber ob sie möglich ist im Rahmen der Berge die wir kennen kann ich nicht sagen, denn ich benötige hiel mehr Wissen als das.
Ich bräuchte die Formel um zu wissen sieviel Schwerkraft auf mich wirkt auf Bodenhöhe.
Nun müsste ich mit der gleichen Formel ausrechnen wieviel Schwerkraft ich sagen wir pro 1 Meter über Bodenhöhe verliere.
Zuletzt müsste ich die Formel so umkehren dass ich weiss wieviel Masse mehr ich unter mir haben müsste um bei 1Meter über Bodenhöhe die gleiche Gravitation zu erfahren wie auf Bodenhöhe.
Und diese Mühe mache ich mir mir trotz meiner starken Neugier jetzt leider nicht
Das hat überhaupt nichts mit der Dichte des Mantels zu tun 🤨
Die Gravitationskraft zwischen zwei Objekten sinkt, je weiter sie voneinander entfernt sind. So einfach ist das.