Hilfe bei Zentralklausur Mathe 2017? (Sachaufgabe, Hochpunkt/Tiefpunkt)? Lösungen?
Ich brauche Hilfe bei den Aufgaben b c und d.
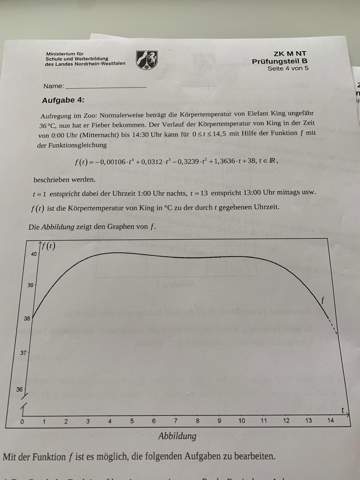
Sachaufgabe zu Extrempunkten (Hochpunkt/Tiefpunkt)

2 Antworten
b (1): 1. Hochpunkt ermitteln (wie man am Graphen sieht, kommt es später noch einmal zu einer Temperaturerhöhung...)
b (2): hier musst Du "alle" Tiefpunkte bestimmen UND die Randwerte, d. h. die Temperaturen um 0:00 Uhr und 14:30 Uhr. Denn wie Du siehst ist der Tiefpunkt nicht die tiefste Temperatur im angegebenen Bereich!
c) berechne das Intervall f(t)>38,5; evtl. f(t)=38,5 ermitteln und dann die Intervalle testen, ob die Werte darin > oder < 38,5 sind; es fällt meist leichter mit Gleichungen als mit Ungleichungen zu rechnen, weil man bei Ungleichungen oft evtl. Fallunterscheidungen vergißt, oder die >, <-Zeichen falsch setzt (wenn man z. B. durch einen negativen Wert teilt oder damit multipliziert)
d) die Steigung bei x=14,5 (=14:30 Uhr) ermitteln und dann ausrechnen (ausgehend vom Funktionswert f(14,5), wann bei dieser ermittelten Steigung der Wert 36 erreicht ist...
Das ist tatsächlich schwierig (habe mir den Term erst nicht so genau angeguckt), da man weder t ausklammern noch mal eben was raten kann. Entweder dürft ihr das mit entsprechenden Taschenrechnern ermitteln, oder Du musst mit Annäherung arbeiten. Dazu musst Du erst mit Wertetabellen schauen, wo f'(x) das Vorzeichen wechselt und dann das entsprechende Intervall immer weiter eingrenzen, bis man eine "brauchbare" Annäherung hat. Wo die Extremstellen grob liegen, kann man am Graphen sehen. So liegt der 1. Hochpunkt irgendwo zwischen 3 und 5...
Das ist eine Kurvendiskussion
a) und b) Maximum und Minimum ermitteln
c) f(t)=38,5°=.... 0=.....-38,5°
d) f´(14,3)=m=....
f(t)=-0,00106*t⁴+0,0312*t³-0,3239*t²+1,3636*t+38 abgeleitet
f´(t)=0=-0,00424*t³+0,0936*t²-0,6478*t+1,3636
Nullstellen mit meinem Graphikrechner (GTR,Casio)
t1=10,1087.. und t2=7,9799.. und t3=3,9868..
nun Prüfen,ob ein Maximum oder Minimum vorliegt
noch mal ableiten
f´´(t)=-0,01272*t²+0,1872*t-0,6478
f´´(10,11)=....=-0,055 <0 also ein Maximum
f´´(7,98)=...=0,036> 0 also ein Minimum
f´´(3,97)=...=-0,105 <0 also ein Maximum
c) f(t)=38,5°=.....
0=.....-38,5°
d) Steigung an der Stelle f´(14,3°)=m=... ausrechnen
Tangengentengleichung yt=ft(x)=fxo´(xo)*(x-xo)+f(xo)
xo=Stelle,wo die Tangente liegen soll
hier t=14,3 Std xo=14,3
Hier Infos per Bild Kurvendiskussion.

Hier Herleitung Tangentengleichung/Normalengleichung



Und wie ermittel ich hierbei den Hochpunkt bei b (1)oder Tiefpubkt bei b (2)?