Hilfe bei Käthe aufgabe. Wie sind die Lösungen,kann mir das bitte jemand sagen? ? Bitte mit Lösungsweg .....?
Falls das Bild nicht angezeigt wird.... Ich habe hier zwei rechtwinklige Dreiecke. Beim ersten muss ich die Hypotenuse ausrechnen die Katheten sind 4,9 und 2,5 Cm lang. Beim zweiten ist die Kathete gefragt. Die andere Kathete ist 3,7 cm und die Hypotenuse ist 9,4 cm lang. Bitte um Lösung mit lösungs weg
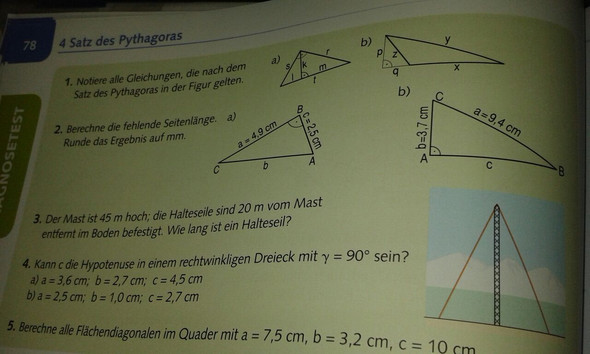
5 Antworten
b = wurzel(4,9² + 2,5²)
Was dich wahrscheinlich irritiert sind die abartigen Beschriftungen der Dreiecke.
Hier mal ein Bild, wo gezeigt wird, wie rechtwinklige Dreiecke im deutschen Sprachraum beschriftet werden.
http://www.michael-buhlmann.de/Mathematik/images/dreieck01.jpg
Alpha ist am Eckpunkt A
Beta ist am Eckpunkt B
Gamma ist am Eckpunkt C
Aufgabe 2.)
Linkes Dreieck :
b ist c
c ist a
a ist b
Beta ist Gamma
Alpha ist Beta
Gamma ist Alpha
Nach der Umbeschriftung :
Gamma = 90 °
a = 2.5 cm
b = 4.9 cm
c = √(a ^ 2 + b ^ 2)
Alpha = arcsin (a / c)
Beta = arcsin (b / c)
c = √(2.5 ^ 2 + 4.9 ^ 2)
c = √(6.25 + 24.01) = √(30.26) = 5.5 cm (gerundet)
Alpha = arcsin (2.5 / 5.5) = 27 ° (gerundet)
Beta = arcsin (4.9 / 5.5) = 63 ° (gerundet)
Da man umbeschriftet hatte muss man das wieder zurück umbeschriften :
b = 5.5 cm
Beta = 90 °
Gamma = 27 °
Alpha = 63 °
Rechtes Dreieck :
b ist a
a ist c
c ist b
Alpha ist Gamma
Gamma ist Beta
Beta ist Alpha
Nach der Umbeschriftung :
Gamma = 90 °
a = 3.7 cm
c = 9.4 cm
b = √(c ^ 2 - a ^ 2)
Alpha = arcsin (a / c)
Beta = arcsin (b / c)
b = √(9.4 ^ 2 - 3.7 ^ 2)
b = √(88.36 - 13.69) = √(74.67) = 8,6 cm (gerundet)
Alpha = arscin (3.7 / 9.4) = 23,2 ° (gerundet)
Beta = arcsin (√(74.67) / 9.4) = 66,8 ° (gerundet)
Da man umbeschriftet hatte muss man das wieder zurück umbeschriften :
c = 8.6 cm
Beta = 23,2 °
Gamma = 66,8 °
Alpha = 90 °
Du hast ja schon die komplette Lösung stehen. Es gilt beim ersten :
a^2 + c^2 = b^2 | weil die längste Seite gesucht wird
(4,9cm)^2 + (2,5cm)^2 = b^2
Beim zweiten wird eine Kathete gesucht, es gilt :
a^2 -b^2 = c^2
(9,4 cm)^2 - (3,7 cm)^2 = c^2
Ausrechen und fertig !
Achtung : Du musst immer den größten Wert, nehmen sonst bekommst du einen Fehler.
a^2+b^2= c^2
Du hast die Hypotenuse und eine Kathete, sodass c^2-a^2= b^2
Dann Wurzel ziehen sowie runden.
Und nicht vergessen, dass ich andere Seitennamen benutzt habe.
Das habe ich gemacht,aber mein Ergebniss kommt nicht hin,deshalb habe ich ja nach der Lösung gefragt
Wenn du die Namen Kathete und Hypotenuse kennst, ist da nichts abartig, sondern alles ganz normal.
In Worten bedeutet der Pythagoras:
Wenn ich die Hypotenuse suche, addiere ich die Quadrate der Katheten und ziehe die Wurzel aus der Summe.
Wenn ich die andere Kathete suche, subtrahiere ich die Quadrate von Hypotenuse und der gegebenen Kathete und ziehe die Wurzel aus der Differenz.