Hilfe bei dieser Mathe aufgabe Orthogonale Matrizen?
Guten tag ich komme hier bei dieser Aufgabe nicht weiter kann mir es jemand bitte erklären und gegebenfalls berechnen? Ich bedanke mich im Vorraus.

2 Antworten
Die Spaltenvektoren müssen
1) normiert und
2) orthogonal zueinader
sein.
Wir dürfen für a, b und c komplexe Zahlen wählen, sowie die Spalten bzw. Zeilen mit Skalaren multiplizieren.
Wegen 1) muss die zweite Spalte mit 1/√2 multipliziert werden.
Wir bilden nun einmal die drei Skalarprodukte
I) a + b + c = 0
II) –1 + c = 0
III) –b + 1 = 0
Hier können wir sofort c = 1 und b = 1 ablesen. Damit folgt dann a = –2.
Nun müssen wir die erste Spalte noch wegen 1) mit 1/√3 multiplizieren, sowie die dritte mit 1/√6.
Das sollte am Ende so aussehen.
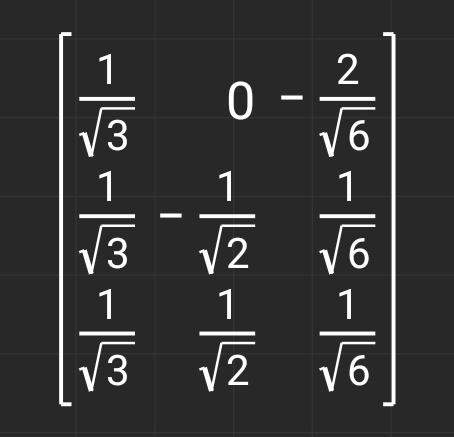
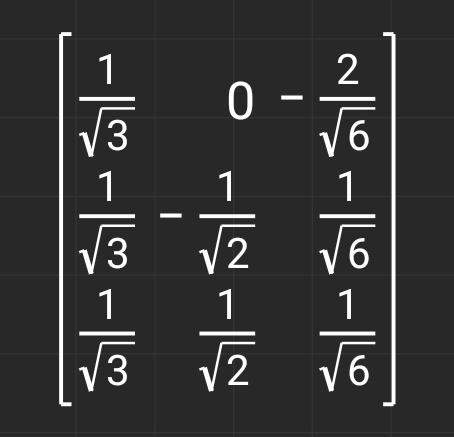
Indem du einfach die Normen (Längen) der Spaltenvektoren berechnest.
Bei der zweiten erhälst du ja
√(0² + (–1)² + 1²) = √2.
Wenn du nun also die ganze Spalte mit dem Kehrwert, also 1/√2, multiplizierst, ist deine erhaltene Norm bzw. Länge eins, also der Spaltenvektor normiert.
Multiplizierst du nämlich einen Vektor v mit einem Skalar a, so ist die Länge |a|•||v||.
Die Skalarprodukte der Spalten bzw. Zeilen miteinander müssen Null ergeben, also z.B. für Spalten 1 und 2
1 * 0 + 1 * (-1) + c * 1 = 0,
was man nach c auflösen kann (c=1).
Mit Spalten 2 und 3 kommt man auf b=1.
Mit Spalte 1 und 3 kommt man auf a = -2.
Jetzt muss man auch noch die Zeilen checken, und diese evtl. mit einem Faktor multiplizieren, damit sich auch hier immer das Skalarprodukt Null ergibt.
Woher weiß man, dass man jetzt zb. 1/√2 benutzen muss um es so zu normieren?