Hi kann mir jemand helfen bei dieser Frage?
Elektra will in ihr Steuergerät 3 LEDs in den Farben blau, gelb und rot einbauen. Wie viele Möglichkeiten hat sie, die Farben anzuordnen?
die Antwort ist 6 aber warum ?
wieso rechnet man dann mal und nicht plus ?
2 Antworten
Es gibt 3 Möglichkeiten, welche der LEDs sie an erster Position verbaut.
Für jede dieser 3 Möglichkeiten gibt es jeweils Möglichkeiten, welche der beiden verbleibenden LEDs sie an zweiter Position verbaut. Das macht bis dahin dann insgesamt 3 ⋅ 2 = 6 Möglichkeiten.
Für die letzte Position bleibt dann nur noch eine LED übrig. Da gibt es dann jeweils nur noch eine Möglichkeit, sodass man dann insgesamt auf...
... Möglichkeiten kommt.
============
Allgemein lässt sich die Anzahl der Möglichkeiten n unterscheidbare Objekte auf n verschiedene Positionen zu verteilen durch n! (sprich: „n Fakultät“) berechnen...
Im konkreten Fall mit n = 3...
============
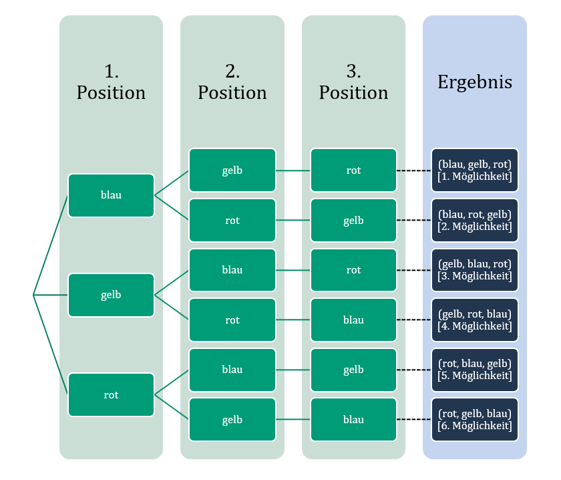
Ansonsten könntest du im konkreten Fall auch ein Baumdiagramm zeichnen und die Möglichkeiten abzählen. [Für größere Zahlen wäre das sehr aufwändig. Aber im konkreten Fall hält sich der Aufwand in Grenzen.]
wieso rechnet man dann mal und nicht plus ?
Weil man nicht einfach 3 Möglichkeiten und zusätzlich 2 andere Möglichkeiten hat, sodass man dann 3 + 2 Möglichkeiten hätte.
Sondern man hat für jede der 3 Möglichkeiten jeweils 2 Möglichkeiten.
Sieh es so... Es gibt 3 Fälle mit jeweils 2 Möglichkeiten. Du hast also 2 Möglichkeiten für den ersten Fall, 2 Möglichkeiten für den zweiten Fall, 2 Möglichkeiten für den dritten Fall. Das sind dann insgesamt 2 + 2 + 2 = 6 Möglichkeiten. Wobei man dann statt 2 + 2 + 2 auch 3 ⋅ 2 schreiben bzw. rechnen kann.
Evtl. hast du meinen Kommentar unter der Antwort noch nicht gesehen gehabt? Oder hast du diesen gesehen, und dir ist das weiterhin nicht klar?
Vielleicht schaust du dir auch das Baumdiagramm am Ende meiner Antwort nochmal an.
Zu Beginn hast du 3 Verzweigungen (3 Möglichkeiten). Hinter jeder dieser 3 Verzweigungen hast du jeweils nochmal 2 Verzweigungen (also jeweils 2 Möglichkeiten für jede der 3 vorigen Möglichkeiten).
Wie viele Fälle hast du dann insgesamt? 3 ⋅ 2 = 2 + 2 + 2 = 6 Fälle oder 3 + 2 = 5 Fälle?
Wie meinst du das mit weil man nicht einfach 3 Möglichkeiten und zusätzlich 2 Möglichkeiten hat, sodass man 3+2 Möglichkeiten hätte ?
Dass man nicht einfach addieren kann.
------------
Ein Beispiel, bei dem man addieren könnte...
Es befinden sich 9 durchnummerierte Kugeln in einer Urne. Die Kugeln 1, 2, 3 sind rot. Die Kugeln 4, 5 sind grün. Die Kugel 6, 7, 8, 9 sind blau. Wie viele verschiedene Möglichkeiten gibt es beim Ziehen einer Kugel eine Kugel zu ziehen, die nicht blau ist?
Da hätte man beispielsweise 3 Möglichkeiten für eine rote Kugel und 2 Möglichkeiten für eine grüne Kugel. Zusammen dann 3 + 2 = 5 Möglichkeiten.
Hier sind es beispielsweise nicht 3 ⋅ 2 = 6 Möglichkeiten. Denn man hat ja nicht für jede der 3 Möglichkeiten (für rote Kugeln) jeweils 2 Möglichkeiten (für grüne Kugeln). Sondern die 3 Möglichkeiten und die 2 Möglichkeiten sind einfach Möglichkeiten, die separat voneinander existieren und zusammen insgesamt 5 Möglichkeiten ergeben.
------------
Und mit dem von dir genannten Satz in meinem Kommentar meinte ich, dass man eben nicht solch ein Beispiel (wie hier mein Urnen-Beispiel) vorliegen hat.
Wie viele Möglichkeiten für die erste?
Für jede davon wie viele für die zweite?
Und dann?
wieso rechnet man mal und nicht plus ?