Gibt es Anormale Quaternionen?
Hallo!
Ich lerne zurzeit die anormal komplexen Zahlen, aber auch die Quaternionen. Ich wollte jetzt fragen, ob es eine Zahlenmenge gibt, die wie bei den Quaternionen 2 imaginäre Einheiten hinzufügt, die aber Quadriert 1 ergeben. Also z.B. so:
1² = 1
j² = k² = l² = jkl = 1
Und wenn es so eine Menge nicht gibt, könnte man sie definieren? Und wenn es so eine Menge gibt: Gibt es die auch mit den Sedenionen?
Danke!
1 Antwort
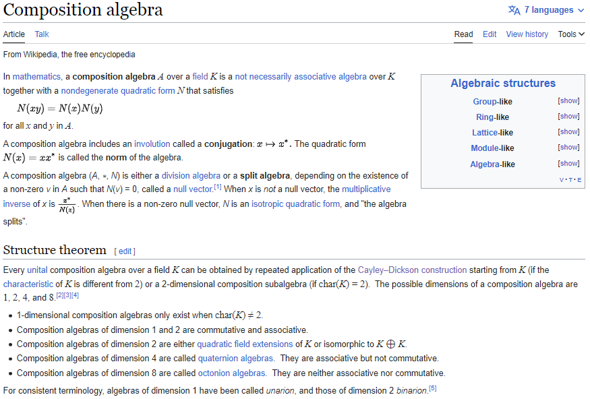
Es gibt etwas ähnliches Namens Split-Quaternionen. Sie sind eine Untermenge der Split-Algebren (Algebren von Zahlen mit imaginären Einheiten deren Quadrat negativ ist, wobei das negative mit der Gegenzahl ersetzt wurde)! Man nennt diese Algebren auch Kompositions-Algebren.
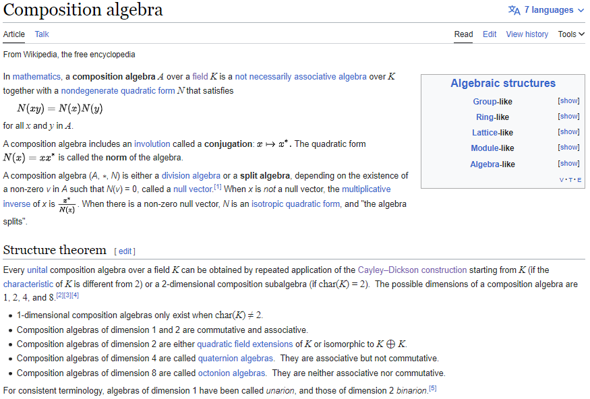
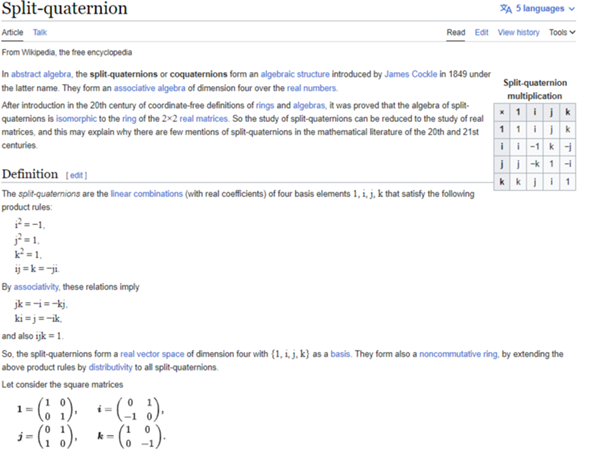
Diese Split-Quaternionen haben imaginäre Einheiten gegeben durch:
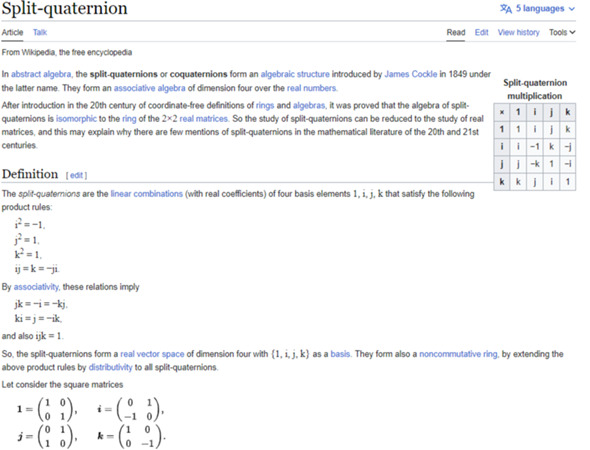
Somit erfüllen sie deine Definition.
PS
Bitte sag nicht Anormale ...
Die nennt man nur in deutschen so. Aber es gibt keinen guten Grund dafür. In fast allen anderen Sprachen wo ich die gesehen habe schreibt man die mit Split--...
Ich weiß net wer sich das mit Anormal ausgedacht hat.
PPS
Mehr Verallgemeinerungen kannst du auch hier finden: https://math.stackexchange.com/q/4674642/1103878
Ok. Ich finde "Anormal" auch nicht so schön.
Danke!
PPPS... Ich könnte auch mal diese Wikipedia Artikel auf Deutsch übersetzen.