Frage zur Wahrscheinlichkeitsrechnung, Beispiel an Äpfeln?
hey, ich stelle mich gerade ein wenig dumm an. Die Aufgabe ist die folgende: Man hat 4 Äpfel, davon sind 2 mit Würmern befallen. Ich nehme nun mit einem Griff 2 Äpfel heraus. Mit welcher Wahrscheinlichkeit sind beide Äpfel mit Würmern befallen?
Welche Formel benutze ich hier genau?
4 Antworten
Nummeriere die Äpfel einfach mal für dich durch: 1 und 2 sollen mit Würmern befallen sein, 3 und 4 nicht.
Als nächstes überlegst du dir, wie viele Kombinationen vorkommen können. Das sind hier sechs Kombinationen (1 und 2, 1 und 3, 1 und 4, 2 und 3, 2 und 4, 3 und 4). Nur in einem dieser Fälle, nämlich 1 und 2, sind beide Äpfel befallen.
Da alle Möglichkeiten gleich wahrscheinlich sind, beträgt die gesuchte Wahrscheinlichkeit also 1/6.
Hallo,
das kannst Du mit dem Binomialkoeffizienten 4 über 2 (Taschenrechner: 4nCr6) lösen. Es gibt sechs Möglichkeiten, wie die zwei wurmstichigen auf vier Äpfel verteilt sein können. Somit liegt die Chance, die richtige Kombintion zu erwischen, bei 1/6.
Herzliche Grüße,
Willy
nCr. Wenn es so eine Taste bei Dir nicht gibt, rechnest Du mit Fakultäten, also mit der !-Taste:
4 über 2 bedeutet 4!/(2!*2!), also (1*2*3*4)/[(1*2)*(1*2)]
Der Nenner ergibt 4, die kannst Du gegen die 4 im Zähler kürzen, dann bleibt 1*2*3=6 übrig.
Willy
Du hast sechs Möglichkeiten, eine davon mit zwei Würmern. Also ist die Wahrscheinlichkeit 1:6.
Ich habe dir dazu mal eine Skizze gemacht.
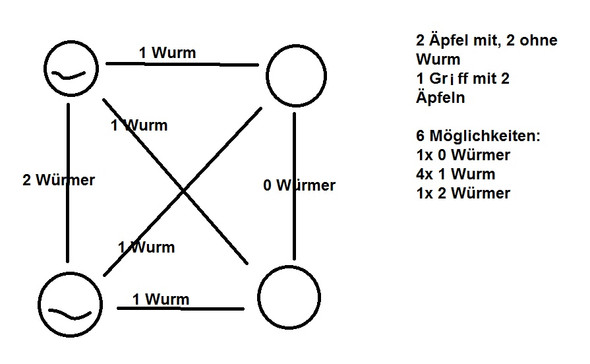
Super danke, mein Fehler war, dass ich die 4 Möglichkeiten nicht bedacht habe, einen schlechten Apfel zu ziehen.
Die Wahrscheinlichkeit beträgt p=0,25
Vorausgesetzt dein Ziehverfahren erwischt jeden Apfel mit der gleichen Wahrscheinlichkeit.
Das ist die Wahrscheinlichkeit dafür, daß Du zweimal hintereinander einen wurmstichigen Apfel aus dem Korb ziehst, wenn Du den ersten nach dem Ziehen wieder zurücklegst.
Das ist laut meinen Lösungen leider falsch. Die korrekte Antwort lautet p=1/6. Ich weiß nur gerade nicht, wie die darauf gekommen sind.
Du hast recht!
Ich hatte das falsche Modell im Kopf.
Modell: "Ziehen ohne Zurücklegen"
Es ist 1/6=2/4*1/3
Stell dir das ganze als zweimal ziehen ohne Zurücklegen vor.
Beim ersten Ziehen ist sind zwei von vier Äpfeln faul, beim zweiten mal einer von dreien.
Ich finde das "über" nicht... habe noch einen ziemlich alten Taschenrechner aus der Schule. Kannst du vielleicht beschreiben, wie das Zeichen aussieht? :)