Flächeninhalt?



Hallo Leute,
Und zwar wollte ich euch fragen ob die Nr. 2a.) stimmt :40-2-8-8-3=19cm Quadrat
Und bei 3a.) wäre meine Frage ob das richtig gezeichnet wurde und wie man den Flächeninhalt und Umfang davon berechnet, könnte mir jemand dort bitte helfen, würde mich sehr über eure Hilfe freuen :)
4 Antworten
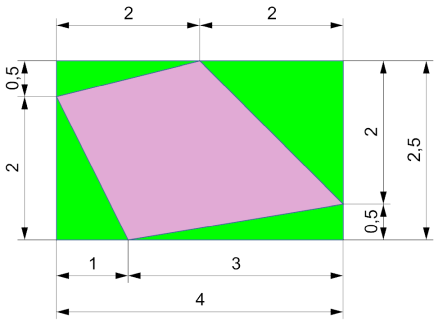
Aufgabe 2a
A1: Rechteck 4x2,5
A1 = 4 * 2,5
A1 = 10 cm²
---
A2: Dreieck 2x0,5
A2 = 2 * 0,5 / 2
A2 = 0,5 cm²
---
A3: Dreieck 2x2
A3 = 2 * 2 / 2
A3 = 2 cm²
---
A4: Dreieck 3x0,5
A4 = 3 * 0,5 / 2
A4 = 0,75 cm²
---
A5: Dreieck 2x1
A5 = 2 * 1 / 2
A5 = 1 cm²
---
Gesamtfläche Figur (lila)
A = A1 - A2 - A3 - A4 - A5
A = 10 - 0,5 - 2 - 0,75 - 1
A = 5,75 cm²
Der Flächeninhalt der Figur 2a
beträgt 5,75 cm²

Danke für die gute veranschaulichung, hat mir sehr geholfen :)
2a)
Fläche umfassendes Rechteck: 5x8 = 40 ( Kästchen )
Fläche Dreieck oben links: 4*1/2 = 2 ( Kästchen )
Fläche Dreieck oben rechts: 4*4/2 = 8 ( Kästchen )
Fläche Dreieck unten links: 4*2/2 = 2 ( Kästchen )
Fläche Dreieck unten rechts: 6*1/2 = 3 ( Kästchen )
Fläche gesamt = 19 ( Kästchen )
Weil 4 Kästchen einem cm^2 entsprechen, beträgt die Fläche 19/4 cm^2.
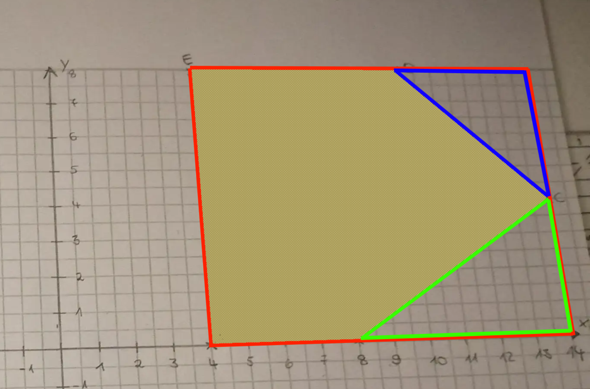
3a)
Zeichnung ist richtig.
Berechnung der Fläche wie bei Aufgabe 2): 8x10 - 4*4/2 - 6*4/2 = 60 cm^2
Umfang: Länge der vertikalen / senkrechten Linien sollte klar sein.
Abstand CD:
sqrt( (Cx-Dx)^2 + (Cy-Dy)^2 ) = sqrt( (14-10)^2 + (4-8)^2 ) = sqrt(32) = 4 * sqrt(2)
Abstand CB:
sqrt( (Cx-Bx)^2 + (Cy-By)^2 ) = sqrt( (14-8)^2 + (4-0)^2 ) = sqrt(52) = 2 * sqrt(13)
Was verstehst Du nicht?
wurzel( (Cx-Bx)^2 + (Cy-By)^2 ) ist die Formel für den Abstand der Punkte [Cx,Cy] und [Bx,By].
Satz des Phytagoras?
c^2 = a^2+b^2
c = wurzel ( a^2+b^2 ) = wurzel( (Cx-Bx)^2 + (Cy-By)^2 )
Bei Aufgabe 2a) habe ich 14 ganze Kästchen gezählt und weitere Teilkästchen, die zusammen 9 ganze Kästchen ergeben. Insgesamt komme ich daher auf 14 + 9 = 23 ganze Kästchen.
4 Kästchen entsprechen 1 cm^2 . Also hätte ich 23/4 = 5,75 cm^2 als Fläche.
Nein also als erstes hab ich den Flächeninhalt von dem Dreieck berechnet =40cm^2 dann die 4 Dreiecke die außen sind und kam somit auf das Ergebnis
Aufgabe 3a)

Das ist richtig eingezeichnet. Wie auch in Aufgabe 2 bestimmst du nun den gesamten Flächeninhalt vom Rechteck und ziehst davon den Flächeninhalt der beiden Dreiecke wieder ab.
Die Längen kannst du aus deiner Zeichnung entnehmen. Die Grundseite vom roten Rechteck geht von 4 bis 14, ist also dann 14-4 = 10 cm lang.
Wurzeln haben wir erst 9 Klasse
Den Umfang kann ich dir nicht zeigen, weil du geschrieben hast du kennst noch keine Wurzeln. Da zu bräuchte man den Satz des Pythagoras für die schrägen Seiten und deshalb Wurzeln.
Mit dem Umfang verstehe ich nicht so ganz