Fläche eines Graphen ohne Funktion bestimmen?
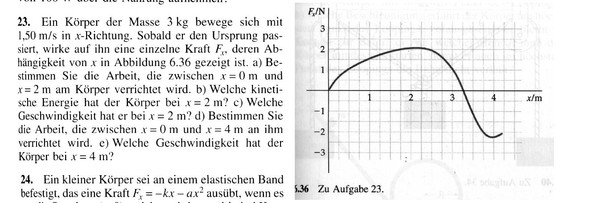
Hey Leute um die Fläche herauszubekommen kann man auch Kästchen zählen. In der Lösung steht: Fläche unter der Kurve 0,125 N pro Kästchen und als Lösung kommt raus W=2,8 J. Meine Frage ist jetzt wie kommt man auf die 0,125 N pro Kästchen und wie gehts dann weiter?
4 Antworten
Das Verfahren nennt man "Planimetrie". Es gibt auch kleine Geräte (Planimeter), nit denen man die Kurve nachfährt und danmit die Fläche bestimmt.
Zur Aufgabe: Wir sollen die Fläche unter der Kurve bestimmen. Deshalb zählen wir die kleinen Quadrate.
Wenn du die Teilfläche 1x1 nimmst, dann zählst du 8 kleine Quadrate in dieser Teilfläche >> also 1 Quadrat = 1/8 der Teilfläche 1x1.
Die Teilfläche 1x1 entsprcht 1 N * 1 m = 1Nm, damit entspricht 1 Quadrat 1/8 Nm = 0,125Nm.
Jetzt noch auszählen und daran denken, dass es auch negativ zählende Quadrate gibt......
Kommst du jetzt weiter?
naja --- pi mal Daumen da kommt man um eine Schätzerei nicht herum, halbes Kästchen, 3/4 Kästchen.... usw
Planimetrie ... hab ich noch nie gehört :)
Wir haben das im Studium mal mit einem Graphen in großem Maßstab gemacht, den ausgeschnitten und das Papier (bzw. die Differenzen) mit einer Briefwage gewogen, um das best. Integral zu erhalten :D
Die Planimetrie kommt aus den Jahren der Rechenschieber. Ich habe sie seinerzeit zum Integrieren von Strom-Spannungskurven genutzt... Das Planimeter war damals unerläßlich. So sahen diese aus: https://www.google.de/search?q=planimeter&ie=utf-8&oe=utf-8&client=firefox-b&gfe_rd=cr&ei=u25vWKeBJ8Ti8AemjbOAAg
Es sind 0,125 Nm pro Kästchen.
Du schaust bei F_x = 1 und x = 1
Das sind in Summe 8 Kästchen ^= 1 Nm =>
1 Kästchen ^= 1/8 Nm bzw 0,125 Nm
Der Rest ist rechnerich ohne Funktion nicht möglich.
Du schaust dir markante Schnittpunkte an wie F_x = 1; x = 0,5 | F_x = 1; x = 1 und unterstellst ein lineares Verhalten und summierst die Flächen.
(Fläche eines Vierecks + Dreieck)
Erstmal guckt man, was der Graph eigentlich darstellt: es geht um die Arbeit W = Kraft F * Weg x . Es kommt als Ergebnis also auf jeden Fall etwas in Nm heraus.
Du betrachtest zunächst das erste Kästchen am Ursprung.
Das hat in y-Richtung den Wert 0,5 N und in x-Richtung den Wert 0,25 m
Multipliziert ergibt das fürs erste Kästchen 0,5 N * 0,25 m = 0,125 Nm
Das ist dann der Wert für alle Kästchen.
Nun zählst du die Kästchen aus.
Dazu kannst du erstmal alle Kästchen zählen, die ganz da sind und nicht durch die Kurve geschnitten werden.
Dann gehst du her und schätzt ab, welche beiden angeschnittenen Kästchen zusammen etwa 1 ganzes Kästchen ergeben. z.B. ergeben das 1. und das 3. angeschnitte Kästchen zusammen 1 ganzes Kästchen. Die beiden streichst du aus und notierst 1 Kästchen. So ziehst du die anderen angeschnittenen Kästchen nach Augenmaß auch zusammen.
Am Ende zählst du alle Kästchen zusammen und multiplizierst sie mit 0,125 Nm
siehe: Bild im Anhang

Vielen Dank wie komme ich aber an die ungenauen Kästchen? Bzw. Wie zähle ich das gibt es da ein Trick?