Fläche berechnen?
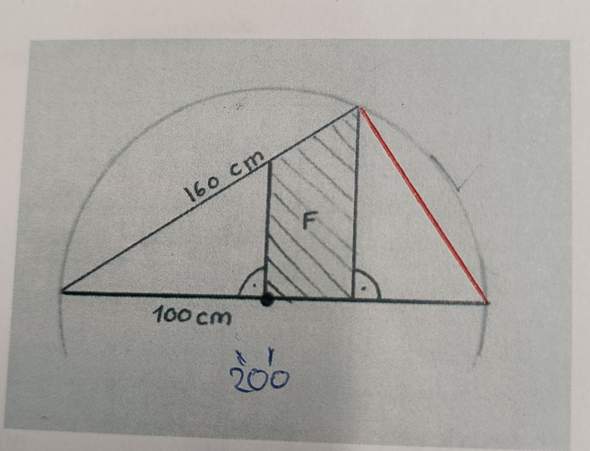
Hallo, ich brauche hilfe um die schraffierte Fläche zu berechnen....Danke :)
4 Antworten
Pythagoras für die rot gekennzeichnete Dreiecksseite (Thaleskreis) und anschließend Strahlensatz (ähnliche Dreiecke), um die Grundseite, Deckseite und Höhe des schraffierten Trapezes zu berechnen. Alternativ: Kathetensatz und Höhensatz, falls das gerade Thema ist.
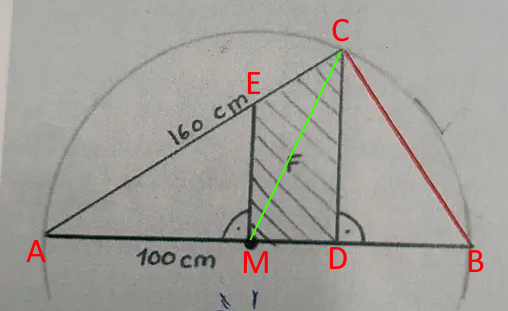
Bestimme Strecke MC, das ist der Radius und 100 cm lang.
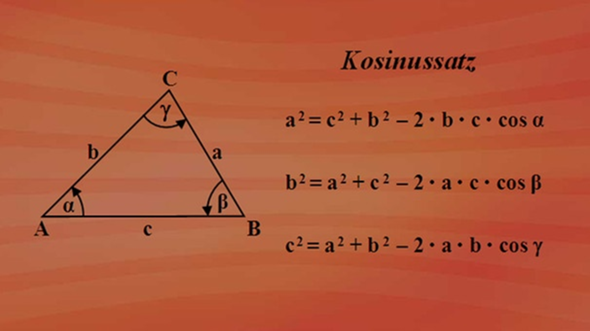
Der Winkel in A also alpha errechnet sich über den Kosinussatz.
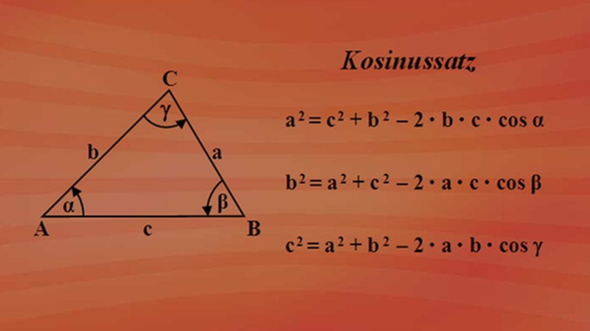
alpha = arccos( (a² - c² - b² ) / (-2 * b * c) =
alpha = arccos((100² - 100² -160²) / (- 2 * 160 * 100)) = 36,87°
tan(36,87°) = ME / AM
ME = AM * tan(36,87°) = 100 * tan(36,87°) = 75 cm
cos(alpha) = AM / AE
AE = AM / cos(alpha) = 100 / cos(36,87°) = 125 cm
EC = 160 - AE = 160 - 125 = 35 cm
Strahlensatz:
MD / CE = AE / AM
MD = AE / AM * CE = 125 / 100 * 35 cm = 43,75 cm
sin(36,87°) = CD / 160
CD = 160 * sin(36,87°) = 96 cm
Fläche F mit der Trapezformel.
F = 0,5 * (ME + CD) * MD = 0,5 * (75 + 96) * 43,75 cm² = 3740,625 cm²
Ohne ein vollständig definiertes Dreieck lässt sich diese Aufgabe nicht eindeutig lösen. Du brauchst entweder noch eine weitere Seitenfläche oder einen Winkel. Oder du verrätst uns, was deine Beschriftung bedeutet.
Ich meine nicht den Aufgabentext sondern die Zahlen und Buchstaben, die die Grafik schmücken und maßgeblich für die Lösung der Aufgabe sind.
Zuerst rechnest du den Flächeninhalt vom großen Dreieck aus. Dann die Flächeninhalte von den kleinen Dreiecken. Rechnest du das Große Dreieck minus die Kleinen solltest du auf die Lösung kommen.
Denke ich zumindest^^
Bei der Beschriftung steht nur, dass ich die Schraffierte Fläche ausrechnen soll und als Tipp noch den Einheitskreis/Strahlensätz aber ich komm nicht drauf.