Fehler beim Trennen der Variablen?

Hallo, beim Separieren der Variablen sieht man häufiger links ein Integral, dessen Stammfunktion der Logarithmus ist:

$\int\frac{d\ y\left(x\right)}{dx}\cdot\frac{1}{y\left(x\right)}\ =\ \ln\left(y\left(x\right)\right)$

Muss es nicht $\ln\left(\mid\ y\left(x\right)\mid\right)\$ sein?

In allen Fällen natürlich +C.

Z.B. folgendes Beispiel von einem prominenten Mathekanal auf YouTube:

$\frac{dy}{y}=\ x\cdot dx$ $\ln\mid y\mid\ \ =\ \frac{1}{2}x^2+C$

Und jetzt die Umformung, die ich nicht verstehe, undzwar:

$y\ =\ e^{\frac{1}{2}x^2+C}$

Mir ist natürlich klar, dass auf beiden Seiten die Basis e genommen wird, um den ln loszuwerden, ich versteh nur nicht, wieso dann das Betragszeichen wegfällt. Mir ist klar, dass der ln nur für positive Werte definiert wird, aber was ist, wenn y negativ ist?

Kann das garnicht sein? Gibt es kein negatives y(x), das dann die DGL löst?

Kann man deswegen schon am Anfang das Betragszeichen weglassen?

Danke im Voraus!

Answer 1

[eterneladam]

Den ln als Stammfunktion gibt es nur zum positiven y, insofern müsste man ausgehend von der DGL

dy/dx = yx

abhängig vom Anfangswert weiter rechnen. In Fall von y(x0) < 0:

dy/dy = (-y)(-x)

dy/(-y) = -x

- ln(-y) = - x² / 2

y = - exp( x² / 2),

worauf man ausgehend vom Fall y(x0) >= 0 auch gleich hätte kommen können.

Answer 2

[verreisterNutzer]

ich versteh nur nicht, wieso dann das Betragszeichen wegfällt. Mir ist klar, dass der ln nur für positive Werte definiert wird, aber was ist, wenn y negativ ist?

... dann lass den Betrag stehen und schau an, was auf der rechten Seite steht. Kann dann y als Funktion von x noch negativ sein? Nein! Also kannst Du die Betragsstriche auch weglassen.

Nachtrag nach Kommentar: Ich skizziere mal y(x) = f(x), vielleicht wird es dann klarer, warum y nicht negativ werden kann.

Comments

[Unbekannt1613]

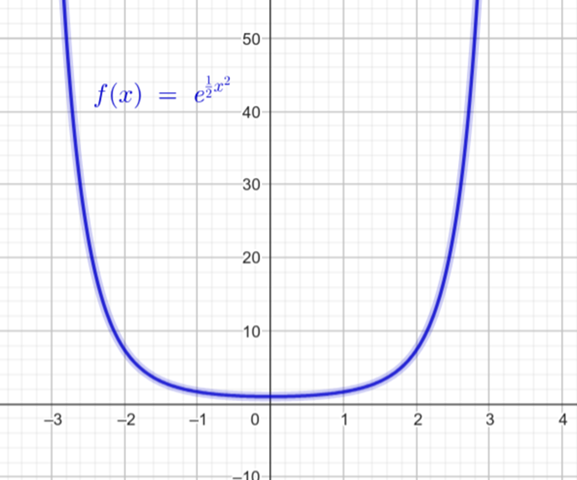
Meinst du exp{1/2 x^2+C} ? Nein das kann nicht Null werden. Aber warum sollte das implizieren, dass y(x) nicht negativ sein kann? Ich bin manchmal etwas langsam, sry..